Dans un précédent article, j’ai abordé les bases de la régression linéaire et de la descente de gradient. Pour mettre en pratique cela, nous allons vous montrer pas à pas une application concrète d’une régression linéaire sur un cas réel avec Scikit-Learn. Ainsi, on va pouvoir appliquer les concepts que nous avons appris sur des données réelles.
Pour aller plus loin, vous pouvez aussi suivre ma MasterClass Data Science et Machine Learning qui comporte plus de 6 heures de contenu vidéo sur la régression linéaire.
Vous êtes prêts à démarrer notre petit projet ?!
C’est parti !
Régression linéaire sur un cas réel : Boston Housing
Nous allons prendre le dataset Boston Housing qui contient des informations sur différentes maisons à Boston. Ces données faisaient à l’origine partie du Machine Learning Repository de l’UCI et ont été supprimées depuis. Nous pouvions également accéder à ces données à partir de la bibliothèque scikit-learn, mais cela va être déprécié dans le futur. Du coup, on y accèdes via ce site web : http://lib.stat.cmu.edu/datasets/boston.
Brièvement, ce dataset contient 506 échantillons et 13 variables de features / caractéristiques. L’objectif est de prédire la valeur du prix des maison en utilisant les features données.
Alors, commençons !
Vous pouvez accompagner la lecture directement avec le code du notebook.
Importations des bibliothèques
Tout d’abord, nous allons importer les bibliothèques classiques d’un projet de Data Sciencce.
import numpy as np import matplotlib.pyplot as plt import pandas as pd import seaborn as sns
Les données
Extraction des données depuis un lien web
Ensuite, nous allons charger les données du Boston Housing à partir d’un site web :
data_url = "http://lib.stat.cmu.edu/datasets/boston" raw_df = pd.read_csv(data_url, sep="\s+", skiprows=22, header=None) data = np.hstack([raw_df.values[::2, :], raw_df.values[1::2, :2]]) target = raw_df.values[1::2, 2] columns = ['CRIM','ZN','INDUS','CHAS','NOX','RM','AGE','DIS','RAD','TAX','PTRATIO','B','LSTAT']
Quelques petites explications :
- pour extraire les valeurs brutes, on passe quelques lignes de description dans le dataset
- puis on concatène les données (pour un tableau NumPy) selon l’axe des colonnes avec hstack
- on extrait la variable cible ou target (le prix des maisons)
- et enfin on liste toutes les colonnes de la description
Description des colonnes
D’ailleurs, en parlant de description, on y trouve une définition pour chaque feature / caractéristique. On a les colonnes suivantes :
- CRIM : Taux de criminalité par habitant par ville.
- ZN : Proportion de zones de terrains résidentiels pour des lots de plus de 25 000 pieds carrés.
- INDUS : Proportion d’acres d’entreprises non commerciales par ville
- CHAS : Variable Dummy Charles River (= 1 si la parcelle borde la rivière ; 0 sinon)
- NOX : concentration d’oxyde nitrique (parties par 10 millions)
- RM : Nombre moyen de pièces par logement
- AGE : Proportion de logements occupés par leur propriétaire construits avant 1940
- DIS : Distances pondérées par rapport à cinq centres d’emploi de Boston
- RAD : Indice d’accessibilité aux autoroutes radiales
- TAX : Taux d’imposition foncière sur la pleine valeur par 10 000 $
- PTRATIO : ratio élèves/professeurs par ville
- B : 1000(Bk – 0.63)², où Bk est la proportion de [personnes d’origine afro-américaine] par ville.
- LSTAT : Pourcentage de la population de statut inférieur
- MEDV : Valeur médiane (ou prix) des maisons occupées par leur propriétaire, en milliers de dollars.
Le prix de la maison indiqué par la variable MEDV est notre variable cible (target) et les autres sont les variables prédictives (features) sur la base desquelles nous allons prédire le prix d’une maison.
Création du DataFrame de données
Nous allons maintenant charger les données dans un DataFrame pandas en utilisant pd.DataFrame. Nous imprimons ensuite les 5 premières lignes des données en utilisant .head().
boston = pd.DataFrame(data=data,columns=columns) boston.head()
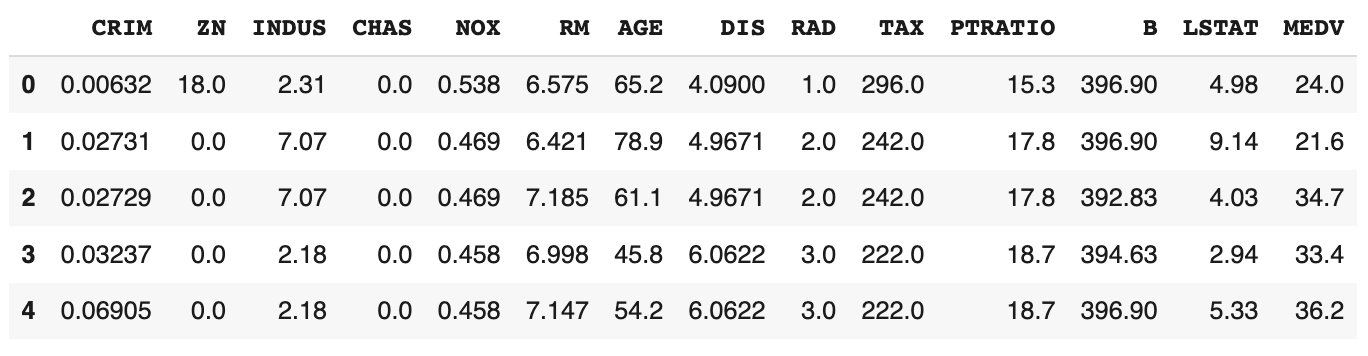
Nous pouvons constater que la variable cible MEDV est absente des données. Nous créons une nouvelle colonne et l’ajoutons au DataFrame :
boston['MEDV'] = target
Pré-traitement des données
Après avoir chargé les données, il est bon de vérifier s’il y a des valeurs manquantes dans les données. Nous comptons le nombre de valeurs manquantes pour chaque feature en utilisant .isnull().
boston.isnull().sum()
Cependant, il n’y a pas de valeurs manquantes dans cet ensemble de données, comme le montre le tableau ci-dessous.
Analyse exploratoire des Données
Distribution de la variable cible
L’analyse exploratoire des données est une étape très importante avant l’entraînement du modèle. Dans cette section, nous utiliserons certaines visualisations pour comprendre la relation de la variable cible avec d’autres features.
Commençons par tracer la distribution de la variable cible MEDV. Nous allons utiliser la fonction displot() de la bibliothèque seaborn.
sns.displot(data=boston,x='MEDV', bins=30,kde=True);
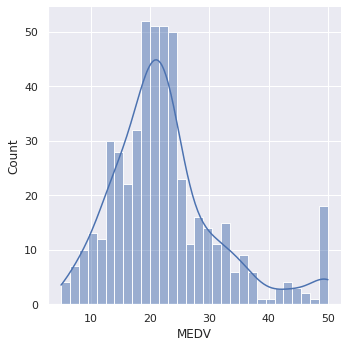
Nous constatons que les valeurs de MEDV sont distribuées normalement avec peu de valeurs aberrantes (ou outliers).
Matrice de corrélation
Ensuite, nous créons une matrice de corrélation qui mesure les relations linéaires entre les variables. La matrice de corrélation peut être créée à l’aide de la fonction .corr() sur un DataFrame depuis la bibliothèque pandas. Nous utiliserons la fonction heatmap() de la bibliothèque seaborn pour tracer la matrice de corrélation.
correlation_matrix = boston.corr().round(2) sns.heatmap(data=correlation_matrix, annot=True);
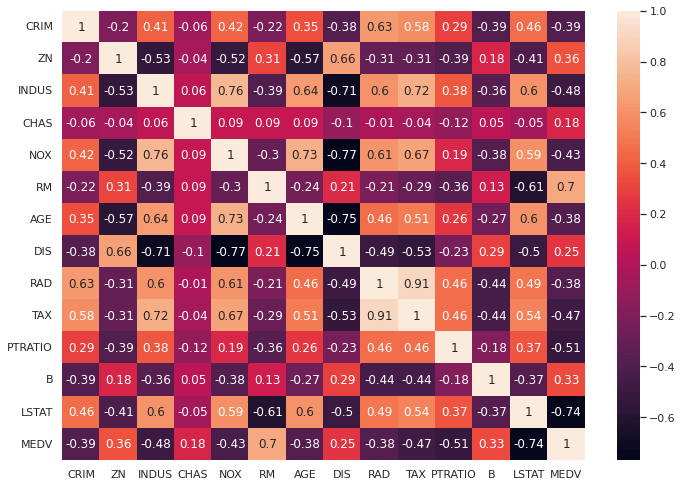
Le coefficient de corrélation varie de -1 à 1. Si la valeur est proche de 1, cela signifie qu’il existe une forte corrélation positive entre les deux variables. Lorsqu’il est proche de -1, les variables ont une forte corrélation négative.
Observations :
- Pour entraîner un modèle de régression linéaire, nous sélectionnons les features qui ont une forte corrélation avec notre variable cible MEDV.
En regardant la matrice de corrélation, nous pouvons voir que RM a une forte corrélation positive avec MEDV (0,7) alors que LSTAT a une forte corrélation négative avec MEDV (-0,74). - Un point important dans la sélection des features pour un modèle de régression linéaire est de vérifier la multi-colinéarité.
Les featuress RAD, TAX ont une corrélation de 0,91. Ces paires de features sont fortement corrélées entre elles. Nous ne devrions donc pas sélectionner ces deux features ensemble pour entraîner le modèle.
Il en va de même pour les features DIS et AGE qui ont une corrélation de -0,75.
Dispersion des features
Sur la base des observations ci-dessus, nous choisirons RM et LSTAT comme features. En utilisant un diagramme de dispersion, voyons comment ces features varient avec MEDV.
plt.figure(figsize=(20, 5))
features = ['LSTAT', 'RM']
target = boston['MEDV']
for i, col in enumerate(features):
plt.subplot(1, len(features) , i+1)
x = boston[col]
y = target
plt.scatter(x, y, marker='o')
plt.title(col)
plt.xlabel(col)
plt.ylabel('MEDV')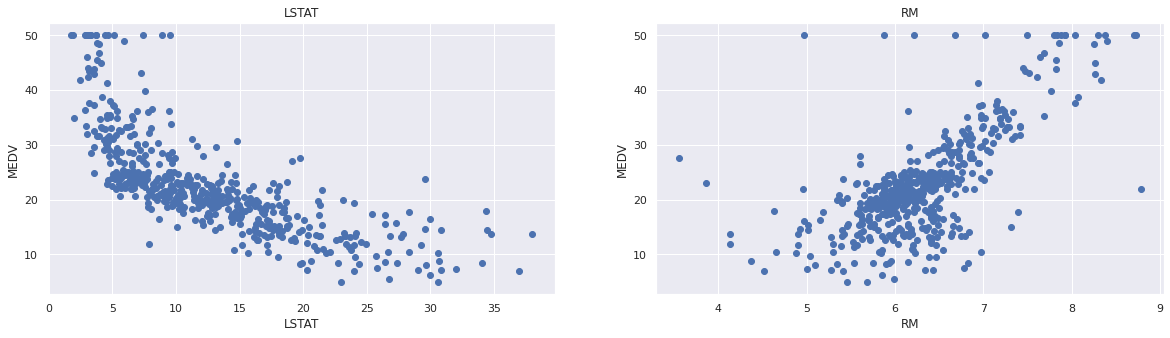
Observations :
- Les prix augmentent lorsque la valeur de RM augmente linéairement. Il y a peu de valeurs aberrantes et les données semblent être plafonnées à 50.
- Les prix ont tendance à diminuer avec une augmentation de LSTAT. Bien que cela ne semble pas suivre exactement une droite linéaire.
Préparation des variables pour le modèle
Création des variables X et y
Nous concaténons les colonnes LSTAT et RM en utilisant np.c_ fourni par la bibliothèque NumPy.
X = pd.DataFrame(np.c_[boston['LSTAT'], boston['RM']], columns = ['LSTAT','RM']) Y = boston['MEDV']
Fractionnement Entraînement / Tests
Ensuite, nous divisons les données en 2 ensembles : d’entraînement et de test. Nous entraînons le modèle avec 70 % des échantillons et le testons avec les 30 % restants. Nous faisons cela pour évaluer la performance du modèle sur des données non vues auparavant par le modèle. Pour séparer les données, nous utilisons la fonction train_test_split() fournie par la bibliothèque scikit-learn. Enfin, nous imprimons les tailles de nos ensembles d’entraînement et de test pour vérifier si le fractionnement s’est produit correctement.
from sklearn.model_selection import train_test_split X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size = 0.3, random_state=101) print(X_train.shape) print(X_test.shape) print(Y_train.shape) print(Y_test.shape)
(354, 2) (152, 2) (354,) (152,)
Mise à l’échelle des données
Il existe différentes façons de mettre à l’échelle vos données, entre autres standardisation et normalisation. Ce n’est pas obligatoire ici, mais prenons l’habitude de le faire pour ne jamais oublier. On va appliquer une mise à l’échelle de standardisation qui ramène nos valeurs entre 0 et 1.
from sklearn.preprocessing import StandardScaler scaler = StandardScaler()
On adapte l’objet de mise à l’échelle (scaler) à nos données d’entraînement uniquement (c’est important !).
scaler.fit(X_train)
Puis on met à l’échelle les features X de nos 2 ensembles de données : Entraînement et Test.
X_train = scaler.transform(X_train) X_test = scaler.transform(X_test)
Notre modèle de régression linéaire
Nous utilisons la fonction LinearRegression de Scikit-learn pour entraîner notre modèle sur l’ensemble d’entraînement.
Création du modèle
from sklearn.linear_model import LinearRegression linear_model = LinearRegression()
Entraînement du modèle
linear_model.fit(X_train, Y_train)
Évaluation du modèle
Nous évaluerons notre modèle en utilisant la racine carrée de l’erreur quadratique moyenne RMSE et le score R2.
from sklearn.metrics import mean_squared_error, r2_score
# évaluation du modèle pour l'ensemble d'entraînement
y_train_predict = linear_model.predict(X_train)
rmse = (np.sqrt(mean_squared_error(Y_train, y_train_predict)))
r2 = r2_score(Y_train, y_train_predict)
print("La performance du Modèle pour le set de Training")
print("------------------------------------------------")
print("l'erreur RMSE esst {}".format(rmse))
print('le score R2 est {}'.format(r2))
print("\n")
# évaluation du modèle pour le set de tesst
y_test_predict = linear_model.predict(X_test)
# racine carrée de l'erreur quadratique moyenne du modèle
rmse = (np.sqrt(mean_squared_error(Y_test, y_test_predict)))
# score R carré du modèle
r2 = r2_score(Y_test, y_test_predict)
print("La performance du Modèle pour le set de Test")
print("--------------------------------------------")
print("l'erreur RMSE est {}".format(rmse))
print('le score R2 score est {}'.format(r2))La performance du Modèle pour le set de Training ------------------------------------------------ l'erreur RMSE esst 5.295854554553106 le score R2 est 0.6358519563974279 La performance du Modèle pour le set de Test -------------------------------------------- l'erreur RMSE est 6.044926081535136 le score R2 score est 0.6318650681832955
C’est plutôt pas mal comme résultats ! Mais, on pourrait évidemment améliorer ce modèle 🙂
Vous pouvez trouver le notebook complet ici.
Conclusion
Dans ce projet, nous avons appliqué les concepts de la régression linéaire sur l’ensemble de données réels Boston Housing. Je vous recommande d’essayer également d’autres ensembles de données.
Par exemple en regardant ces 2 sites web :
