Les diagrammes bivariés ou à deux variables impliquent la visualisation et l’analyse de la relation entre deux variables simultanément. Ils sont utilisés pour explorer la manière dont deux variables sont liées ou corrélées. Les tracés les plus courants avec Matplotlib sont sns.scatterplot(x,y,data), sns.lineplot(x,y,data) pour les diagrammes de dispersion et les diagrammes linéaires.
Diagramme de régression #
Un diagramme de régression se concentre sur la relation entre deux variables numériques : la variable indépendante (souvent sur l’axe des x) et la variable dépendante (sur l’axe des y). Les points de données individuels sont affichés sous forme de points et l’élément central d’un diagramme de régression est la ligne ou la courbe de régression, qui représente le modèle mathématique le mieux adapté pour décrire la relation entre les variables.
Utilise sns.regplot(x,y,data) pour créer un diagramme de régression.
# Diagramme de régression
plt.figure(figsize=(8, 5))
sns.regplot(x="total_bill", y="tip", data=tips, scatter_kws={"color": "blue"}, line_kws={"color": "red"})
plt.title("Diagramme de régression du pourboire en fonction de la facture totale")
plt.xlabel("Facture totale (en $)")
plt.ylabel("Pourboire (en $)")
plt.show()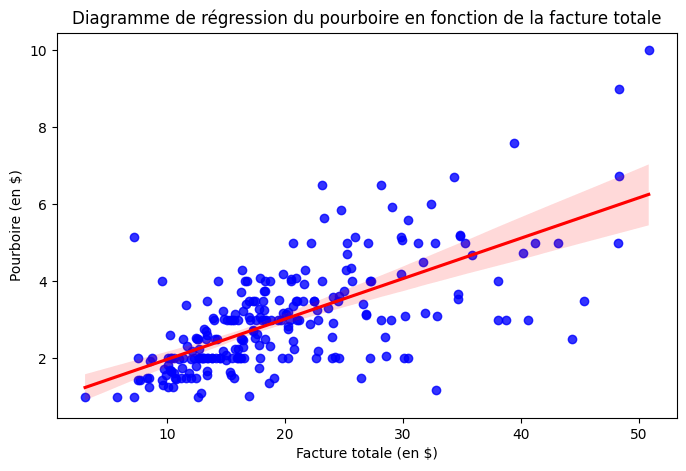
- La droite de régression représente le modèle linéaire le mieux adapté pour prédire les pourboires en fonction du montant total des factures. Les points de dispersion représentent des points de données individuels et tu peux observer comment ils se regroupent autour de la droite de régression. Ce diagramme est utile pour comprendre la relation linéaire entre ces deux variables.
Joint Plot #
Un diagramme conjoint (Joint Plot) combine des diagrammes de dispersion, des histogrammes et des diagrammes de densité pour visualiser la relation entre deux variables numériques. L’élément central d’un diagramme conjoint est un diagramme de dispersion qui affiche les points de données des deux variables l’un par rapport à l’autre. Le long des axes x et y du diagramme de dispersion, il y a des histogrammes ou des diagrammes d’estimation de la densité du noyau (KDE) pour chaque variable individuelle. Ces tracés marginaux montrent la distribution de chaque variable séparément.
Utilise sns.jointplot(x,y,data=dataframe,kind), kind peut être une valeur de cette liste : ['scatter', 'hist', 'hex', 'kde', 'reg', 'resid'].
# Diagramme joint
sns.jointplot(x="total_bill", y="tip", data=tips, kind="scatter")
plt.xlabel("facture totale (en $)")
plt.ylabel("Pourboire (en $)")
plt.show()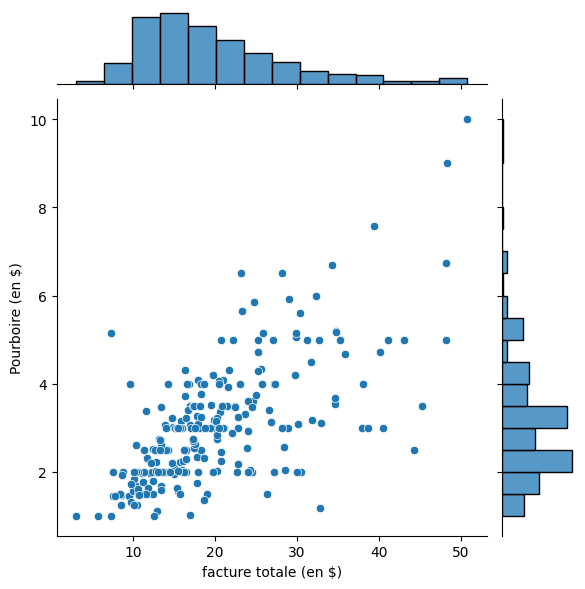
- Comme nous pouvons le voir, cela montre la relation entre les deux variables par le biais d’un diagramme de dispersion, tandis que les histogrammes marginaux montrent la distribution de chaque variable séparément.
Hexbin Plot #
Un diagramme Hexbin (diagramme hexagonal), abréviation de Hexagonal Binning plot, regroupe les points de données dans des cases hexagonales, ce qui permet de visualiser plus efficacement la densité des données et les modèles. Ces tracés sont particulièrement utiles pour les grands ensembles de données, lorsque les diagrammes de dispersion avec des points individuels deviennent trop encombrés et difficiles à interpréter !
Tu peux créer un diagramme hexagonal en utilisant le paramètre kind du Hexbin Plot. Tu peux personnaliser la carte des couleurs, la taille de la grille et d’autres paramètres de tracé pour affiner l’apparence du tracé hexagonal.
# Diagramme hexagonale
plt.figure(figsize=(8, 5))
sns.jointplot(x="total_bill", y="tip",kind='hex', data=tips, gridsize=15, cmap="Blues")
plt.xlabel("Facture totale (en $)")
plt.ylabel("Pourboire (en $)")
plt.show()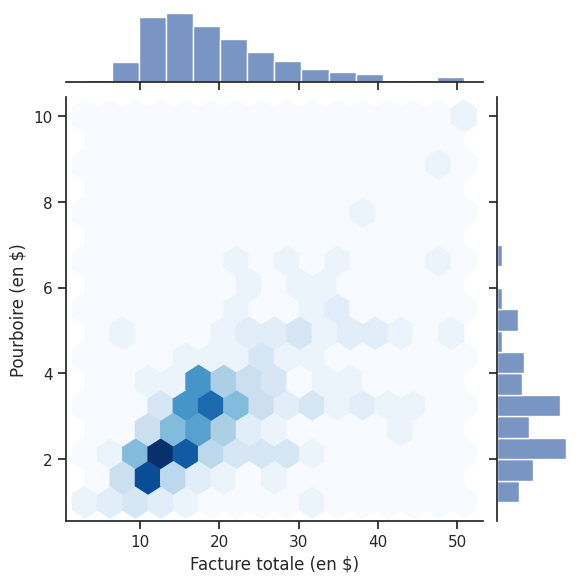
- Cela confirme que le diagramme hexagonal est beaucoup plus clair que le diagramme de dispersion pour un grand ensemble de données. Chaque hexagone du diagramme est codé en couleur pour indiquer la densité des points de données à l’intérieur de cette case hexagonale.




