Prédire le vainqueur de la Coupe du Monde de Football 2022 avec un modèle simple en Python

L’édition 2022 de la coupe du monde FIFA vient tout juste. de démarrer, et pour rester dans le thème de la Data Science et du Machine Learning, j’ai envie d’utiliser toutes les données historiques des matchs des coupes du monde depuis 1930 pour tenter de prédire le vainqueur de la coupe du monde de football 2022 (si tu lis cet article après la remise de la coupe, tu pourras toujours appliquer le modèle prédictif suivant).

Et le vainqueur est…

Beaucoup de gens parlent du football comme d’un jeu imprévisible parce qu’un match de football comporte différents facteurs qui peuvent changer le score final.

C’est vrai… dans une certaine mesure.

Il est difficile de prédire le score final ou le vainqueur d’un match, mais ce n’est pas le cas lorsqu’il s’agit de prédire le vainqueur d’une compétition. Au cours des 5 dernières années, le Bayern Munich a remporté toutes les Bundesligas, tandis que Manchester City a gagné 4 Premiere Leagues.

Une coïncidence ? Je ne pense pas…

Disclaimer : il s’agit d’une prédiction faite avant le début de la coupe du monde.

Comment allons-nous prédire les vainqueurs des différents matchs ?

Il existe différentes façons de faire des prédictions. Je pourrais construire un modèle de Machine Learning sophistiqué et lui fournir de multiples variables, mais après avoir lu quelques articles, j’ai décidé de donner une chance à la distribution de Poisson.

Pourquoi ? Eh bien, regardons la définition de la distribution de Poisson :

La distribution de Poisson est une distribution de probabilité discrète qui décrit le nombre d’événements se produisant dans un intervalle de temps fixe ou une région d’opportunité.

Si nous considérons un but comme un événement susceptible de se produire au cours des 90 minutes d’un match de football, nous pourrions calculer la probabilité du nombre de buts qui pourraient être marqués au cours d’un match par l’équipe A et l’équipe B.

Mais ce n’est pas suffisant. Nous devons encore répondre aux hypothèses de la distribution de Poisson.

1. Le nombre d’événements peut être compté (un match peut compter 1, 2, 3 buts ou plus)
2. L’occurrence des événements est indépendante (l’occurrence d’un but ne doit pas affecter la probabilité d’un autre but)
3. Le rythme auquel les événements se produisent est constant (la probabilité qu’un but se produise dans un certain intervalle de temps doit être exactement la même pour tous les autres intervalles de temps de même longueur)
4. Deux événements ne peuvent pas se produire exactement au même instant (deux buts ne peuvent pas se produire en même temps)

Il ne fait aucun doute que les hypothèses 1 et 4 sont satisfaites, mais les hypothèses 2 et 3 sont partiellement vraies. Cela dit, supposons que les hypothèses 2 et 3 sont toujours vraies.

Si l’on prédit les vainqueurs des principaux championnats européens, l’histogramme du nombre de buts dans chaque match au cours des 5 dernières années nous donne ces tracés ci-dessous pour les 4 principaux championnats.

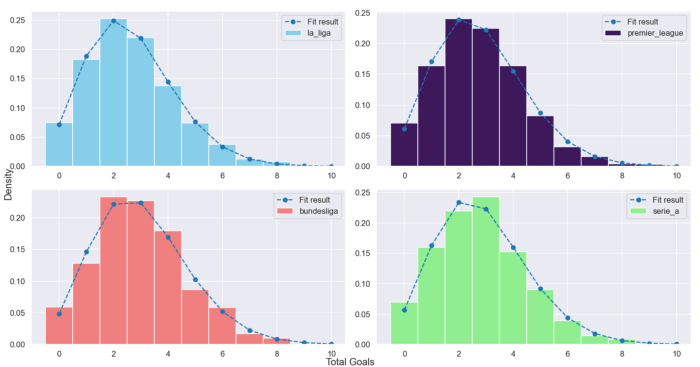
Si tu observes la courbe d’ajustement de n’importe quel championnat, elle ressemble à la distribution de Poisson.

Nous pouvons maintenant dire qu’il est possible d’utiliser la distribution de Poisson pour calculer la probabilité du nombre de buts qui pourraient être marqués lors d’un match.

Voici la formule de la distribution de Poisson :

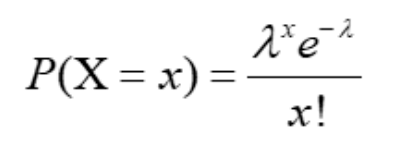
Pour faire les prédictions, j’ai considéré :

• lambda : médiane des buts en 90 minutes (équipe A et équipe B)
• x : nombre de buts dans un match qui pourraient être marqués par l’équipe A et l’équipe B.

Pour calculer lambda, nous avons besoin de la moyenne des buts marqués/concédés par chaque équipe nationale. Cela nous amène au point suivant.

Buts marqués/encaissés par chaque équipe nationale

Après avoir collecté et nettoyé les données de tous les matchs de la Coupe du monde disputés de 1930 à 2018, j’ai pu calculer la moyenne des buts marqués et encaissés par chaque équipe nationale.

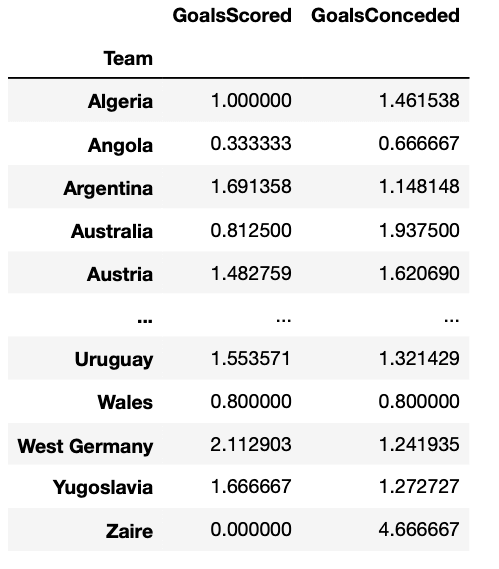
Dans la prédiction que j’ai faite pour les 4 premières ligues européennes, j’ai pris en compte le facteur domicile/extérieur, mais comme dans la Coupe du monde presque toutes les équipes jouent dans un stade neutre, je n’ai pas tenu compte de ce facteur pour cette analyse.

Une fois que j’ai obtenu les buts marqués/encaissés par chaque équipe nationale, j’ai créé une fonction qui prédit le nombre de points que chaque équipe obtiendrait lors de la phase de poule.

Prédire la phase de poule

Tu trouveras ci-dessous le code que j’ai utilisé pour prédire le nombre de points que chaque équipe nationale obtiendrait en phase de poule. Il fait un peu peur, mais en réalité c’est seulement le code qui traduit ce que j’ai mentionné jusqu’à présent.

def predict_points(home, away):
    if home in df_team_strength.index and away in df_team_strength.index:
        lamb_home = df_team_strength.at[home,'GoalsScored'] * df_team_strength.at[away,'GoalsConceded']
        lamb_away = df_team_strength.at[away,'GoalsScored'] * df_team_strength.at[home,'GoalsConceded']
        prob_home, prob_away, prob_draw = 0, 0, 0
        for x in range(0,11): # nombre de buts de l'équipe à domicile
            for y in range(0, 11): # nombre de buts de l'équipe en déplacement
                p = poisson.pmf(x, lamb_home) * poisson.pmf(y, lamb_away)
                if x == y:
                    prob_draw += p
                elif x > y:
                    prob_home += p
                else:
                    prob_away += p
        
        points_home = 3 * prob_home + prob_draw
        points_away = 3 * prob_away + prob_draw
        return (points_home, points_away)
    else:
        return (0, 0)

En clair, predict_points calcule le nombre de points que les équipes à domicile et à l’extérieur obtiendraient. Pour ce faire, j’ai calculé lambda pour chaque équipe en utilisant la formule average_goals_scored * average_goals_conceded.

J’ai ensuite simulé tous les scores possibles d’un match, de 0-0 à 10-10 (ce dernier score est juste la limite de ma gamme de buts). Une fois que j’ai lambda et x, j’utilise la formule de la distribution de Poisson pour calculer p.

Les probabilités prob_home, prob_draw et prob_away cumulent la valeur de p si, par exemple, le match se termine respectivement par 1-0 (victoire à domicile), 1-1 (match nul) ou 0-1 (victoire à l’extérieur). Enfin, les points sont calculés à l’aide de la formule ci-dessous.

points_home = 3 * prob_home + prob_draw
points_away = 3 * prob_away + prob_draw

Si nous utilisons predict_points pour prédire le match Angleterre contre États-Unis, nous obtiendrons ceci.

predict_points('England', 'United States')

(2.2356147635326007, 0.5922397535606193)

Cela signifie que l’Angleterre obtiendrait 2,23 points, tandis que les États-Unis obtiendraient 0,59. J’obtiens des décimales car j’utilise des probabilités.

Si nous appliquons cette fonction predict_points à tous les matchs de la phase de groupe, nous obtiendrons la 1ère et la 2ème nation de chaque groupe.
Voici les résultats :

Groupe A :
– 1er : Equateur
– 2e : Pays-Bas

Groupe B :
– 1er : Angleterre
– 2e Pays de Galles

Groupe C :
– 1er : Argentine
– 2e : Pologne

Groupe D :
– 1er : France
– 2e : Danemark

Groupe E :
– 1er : Allemagne
– 2e : Espagne

Groupe F :
– 1er : Croatie
– 2e : Belgique

Groupe G :
– 1er : Brésil
– 2e : Suisse

Groupe H :
– 1er : Portugal
– 2e : Uruguay

Et donc ensuite, on obtient les matchs suivants à jouer dans la phase des éliminatoires à l’aide du tableau suivant.

Ce qui nous donne les 8 rencontres (prédites) suivantes :

• Equateur – Pays de Galles
• Argentine – Danemark
• France – Pologne
• Angleterre – Pays-Bas
• Allemagne – Belgique
• Brésil – Uruguay
• Croatie – Espagne
• Portugal – Suisse

Prédire les phases éliminatoires

Pour les phases éliminatoires, je n’ai pas besoin de prédire le nombre de points de chaque nation dans son groupe, mais le vainqueur de chaque rencontre éliminatoire (à partir des huitièmes de final). C’est pourquoi j’ai créé une nouvelle fonction get_winner basée sur la fonction predict_points précédente.

def get_winner(df_fixture_updated):
    for index, row in df_fixture_updated.iterrows():
        home, away = row['home'], row['away']
        points_home, points_away = predict_points(home, away)
        if points_home > points_away:
            winner = home
        else:
            winner = away
        df_fixture_updated.loc[index, 'winner'] = winner
    return df_fixture_updated

Pour faire simple, si points_home est supérieur à points_away, le gagnant est l’équipe à domicile, sinon, le gagnant est l’équipe à l’extérieur.

Grâce à la fonction get_winner, je peux obtenir les résultats des rencontres éliminatoires précédentes :

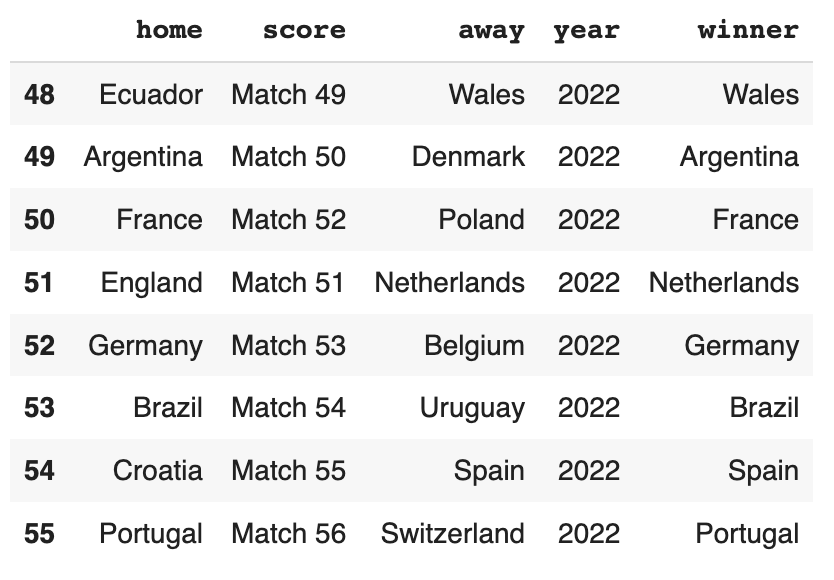
Prédire les quarts de finale, les demi-finales et la finale

Si j’utilise à nouveau get_winner, je peux prédire le vainqueur de la Coupe du Monde.
Voici les résultats :

Quarts de final (prédiction du vainqueur en gras) :
– Allemagne – Brésil
– Pays de Galles – Argentine
– Espagne – Portugal
– Pays-Bas – France

Demi-final :
– Argentine – Brésil
– Pays-Bas – Portugal

Final :
– Brésil – Pays-Bas

En exécutant la fonction une fois de plus, j’obtiens que le gagnant est …

le BRÉSIL !

À noter le beau parcours de notre équipe de France (éliminée en quart de final), cela semble un bon résultat au vu des nombreux blessés français. Mais si ça pouvait nous faire un remake de France – Brésil de 98, on signe de suite 🙂

Cela reste une prédiction statistique en prenant en compte les matchs historiques des précédentes coupes du monde. Mais note bien que cela ne prend pas en compte l’état de forme des équipes ainsi que des blessés (ou éventuelle génération dorée de l’une d’entre elles). Cela fait tout de même ressortir de nombreux « favoris », à savoir le Brésil, l’Argentine, l’Espagne, le Portugal, la France ou encore l’Allemagne.

Voilà, c’est fait ! C’est ainsi que j’ai prédit la Coupe du Monde 2022 en utilisant Python et la distribution de Poisson. Pour voir le code complet, consulte mon notebook sur Google Colab.