Le modèle ARIMA avec Python donne la possibilité de faire des prévisions basées sur des observations historiques, ce qui crée un avantage concurrentiel. Par exemple, si une organisation a la capacité de mieux prévoir les quantités vendues d’un produit, elle sera dans une position plus favorable pour optimiser les niveaux de stock. Cela peut se traduire par une augmentation des liquidités des réserves de trésorerie de l’organisation, une diminution du fonds de roulement et une amélioration de la satisfaction des clients en réduisant l’arriéré des commandes.
Dans le domaine du Machine Learning, il existe un ensemble spécifique de méthodes et de techniques particulièrement bien adaptées pour prédire la valeur d’une variable dépendante en fonction du temps. Dans cet article, nous aborderons la moyenne mobile intégrée autorégressive (ARIMA).
Nous faisons référence à une série de points de données indexés dans l’ordre chronologique comme une série temporelle (time series). Une série temporelle peut être décomposée en 3 composantes.
- Tendance : Mouvement de hausse et de baisse des données au cours du temps sur une longue période (par exemple le prix de l’immobilier)
- Saisonnalité : Variance saisonnière (par exemple une augmentation de la demande de glace pendant l’été)
- Bruit : Des pics et des creux à intervalles aléatoires
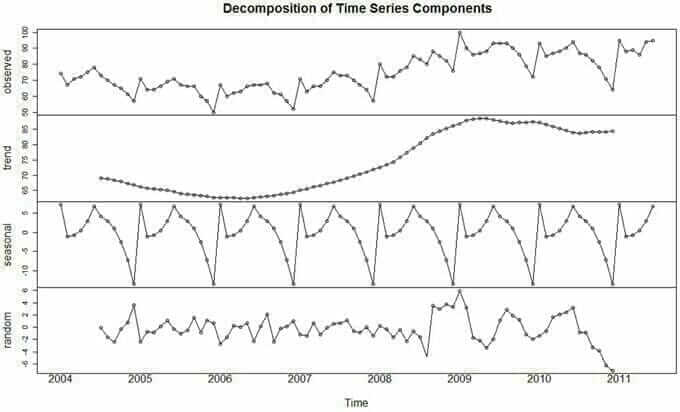
Avant d’appliquer un modèle statistique sur une série temporelle, nous devons nous assurer qu’elle est stationnaire.
Qu’est-ce qu’une série stationnaire ?
1. La moyenne de la série ne doit pas être fonction du temps. Le graphique rouge ci-dessous n’est pas stationnaire car la moyenne augmente avec le temps.
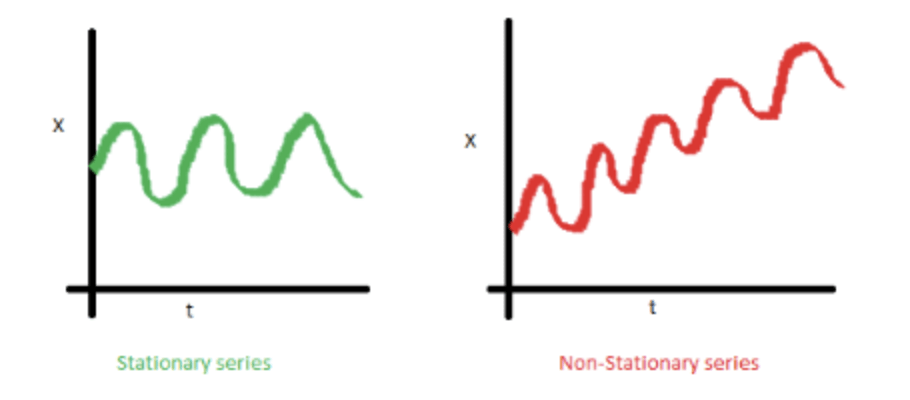
2. La variance de la série ne doit pas être une fonction du temps. Notez dans le graphique rouge ci-dessous la variance des données qui varient dans le temps.
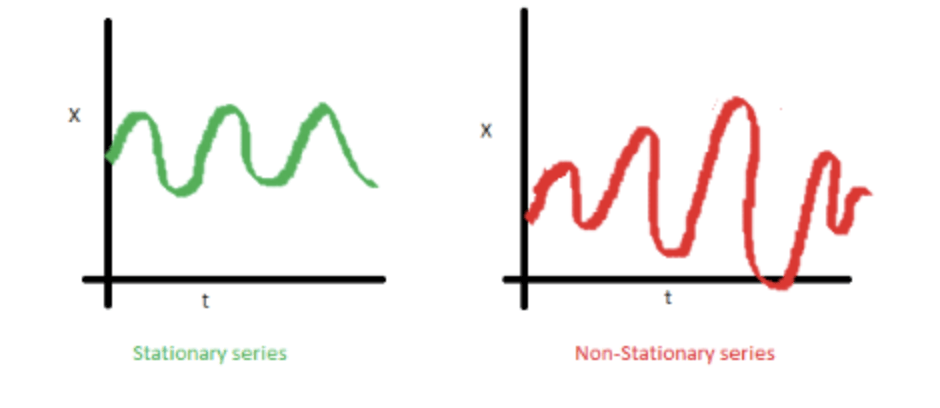
3. Enfin, la covariance du i-ème terme et du (i + m)-ième terme ne doit pas être fonction du temps. Dans le graphique suivant, vous remarquerez que l’écart se rapproche à mesure que le temps augmente. Par conséquent, la covariance n’est pas en rapport avec le temps pour la “série rouge”.
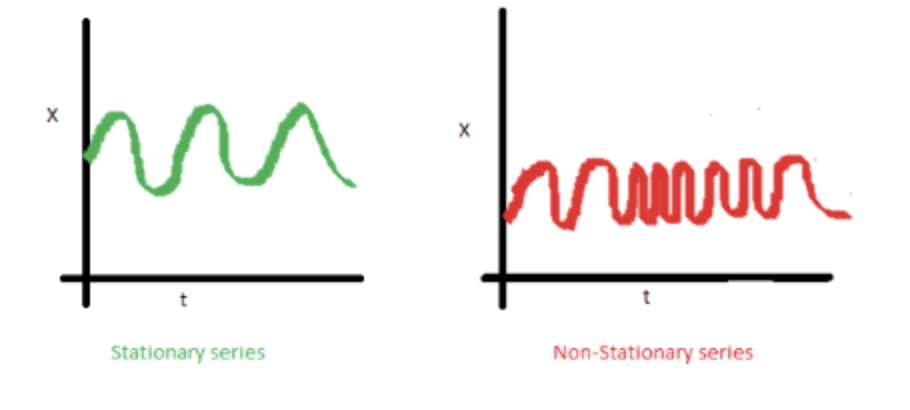
Si une série temporelle est stationnaire et présente un comportement particulier pendant un intervalle de temps donné, on peut supposer sans risque de se tromper qu’elle présentera le même comportement à un moment ultérieur. La plupart des méthodes de modélisation statistique supposent ou exigent que la série temporelle soit stationnaire.
Code Modèle ARIMA avec Python
La bibliothèque statsmodels offre un ensemble de fonctions permettant de travailler avec des données de séries temporelles.
import numpy as np import pandas as pd from matplotlib import pyplot as plt from statsmodels.tsa.stattools import adfuller from statsmodels.tsa.seasonal import seasonal_decompose from statsmodels.tsa.arima_model import ARIMA from pandas.plotting import register_matplotlib_converters register_matplotlib_converters()
Nous allons travailler avec un ensemble de données qui contient le nombre de passagers aériens pour un jour donné. Vous pouvez le télécharger en cliquant ici.
df = pd.read_csv('airline_passengers.csv', parse_dates = ['Month'], index_col = ['Month'])
df.head()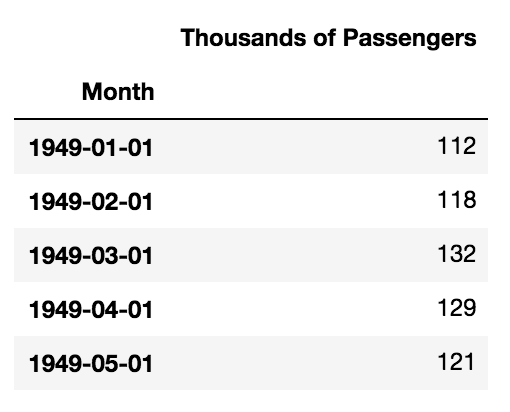
plt.xlabel('Date')
plt.ylabel('Nombre de passagers aériens')
plt.plot(df)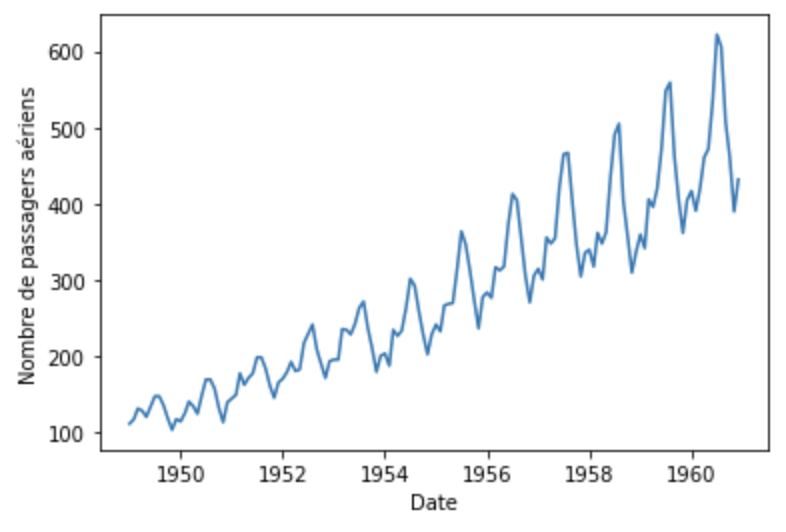
Comme mentionné précédemment, avant de pouvoir construire un modèle, nous devons nous assurer que la série temporelle est stationnaire. Il y a deux façons principales de déterminer si une série temporelle donnée est stationnaire:
- Statistiques roulantes : Tracer la moyenne mobile et l’écart-type mobile. La série temporelle est stationnaire si elle reste constante dans le temps (à l’œil nu, regardez si les lignes sont droites et parallèles à l’axe des x)
- Test de Dickey-Fuller augmenté (ADF) : La série temporelle est considérée comme stationnaire si la valeur p est faible (selon l’hypothèse nulle) et si les valeurs critiques à des intervalles de confiance de 1%, 5%, 10% sont aussi proches que possible des statistiques de l’ADF (Augmented Dickey-Fuller)
Pour ceux qui ne comprennent pas la différence entre la moyenne et la moyenne mobile, une moyenne mobile sur 10 jours calcule la moyenne des prix de clôture des 10 premiers jours comme premier point de données. Et ainsi de suite pour chaque point de donnée suivante.
rolling_mean = df.rolling(window = 12).mean()
rolling_std = df.rolling(window = 12).std()
plt.plot(df, color = 'blue', label = 'Origine')
plt.plot(rolling_mean, color = 'red', label = 'Moyenne mobile')
plt.plot(rolling_std, color = 'black', label = 'Ecart-type mobile')
plt.legend(loc = 'best')
plt.title('Moyenne et Ecart-type mobiles')
plt.show()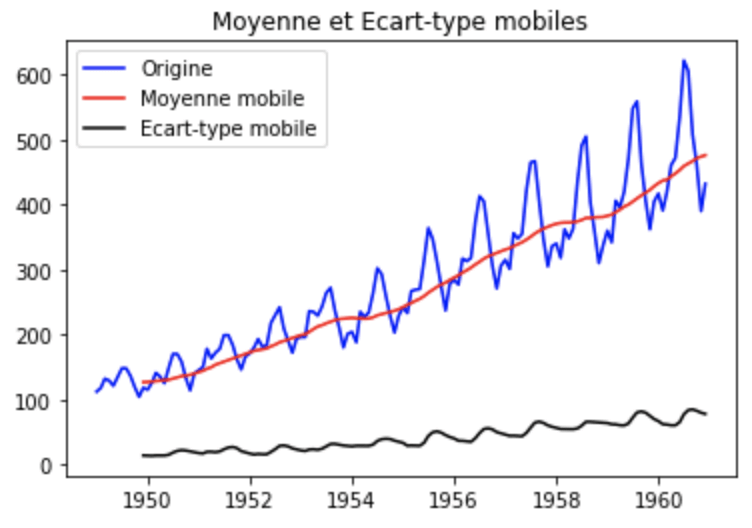
Comme vous pouvez le voir, la moyenne mobile et l’écart-type mobile augmentent avec le temps. Nous pouvons donc conclure que la série temporelle n’est pas stationnaire.
result = adfuller(df['Thousands of Passengers'])
print('Statistiques ADF : {}'.format(result[0]))
print('p-value : {}'.format(result[1]))
print('Valeurs Critiques :')
for key, value in result[4].items():
print('\t{}: {}'.format(key, value))
La statistique ADF est loin des valeurs critiques et la p-value est supérieure au seuil (0,05). On peut donc conclure que la série temporelle n’est pas stationnaire.
Prendre le logarithme de la variable dépendante est un moyen simple de réduire le taux d’augmentation de la moyenne mobile :
df_log = np.log(df) plt.plot(df_log)
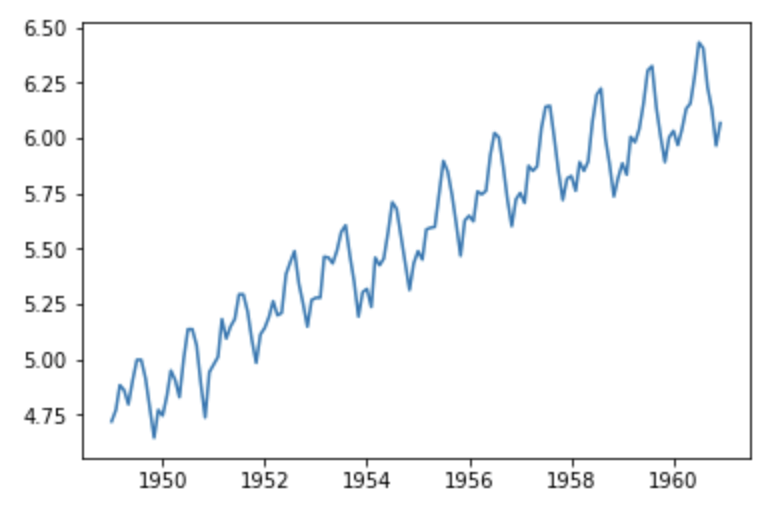
Créons une fonction permettant d’exécuter les deux tests qui déterminent si une série temporelle donnée est stationnaire :
def get_stationarity(timeseries):
# Statistiques mobiles
rolling_mean = timeseries.rolling(window=12).mean()
rolling_std = timeseries.rolling(window=12).std()
# tracé statistiques mobiles
original = plt.plot(timeseries, color='blue', label='Origine')
mean = plt.plot(rolling_mean, color='red', label='Moyenne Mobile')
std = plt.plot(rolling_std, color='black', label='Ecart-type Mobile')
plt.legend(loc='best')
plt.title('Moyenne et écart-type Mobiles')
plt.show(block=False)
# Test Dickey–Fuller :
result = adfuller(timeseries['Passengers'])
print('Statistiques ADF : {}'.format(result[0]))
print('p-value : {}'.format(result[1]))
print('Valeurs Critiques :')
for key, value in result[4].items():
print('\t{}: {}'.format(key, value))Il existe de multiples transformations que nous pouvons appliquer à une série temporelle pour la rendre stationnaire. Par exemple, soustraire la moyenne mobile :
rolling_mean = df_log.rolling(window=12).mean() df_log_minus_mean = df_log - rolling_mean df_log_minus_mean.dropna(inplace=True)get_stationarity(df_log_minus_mean)
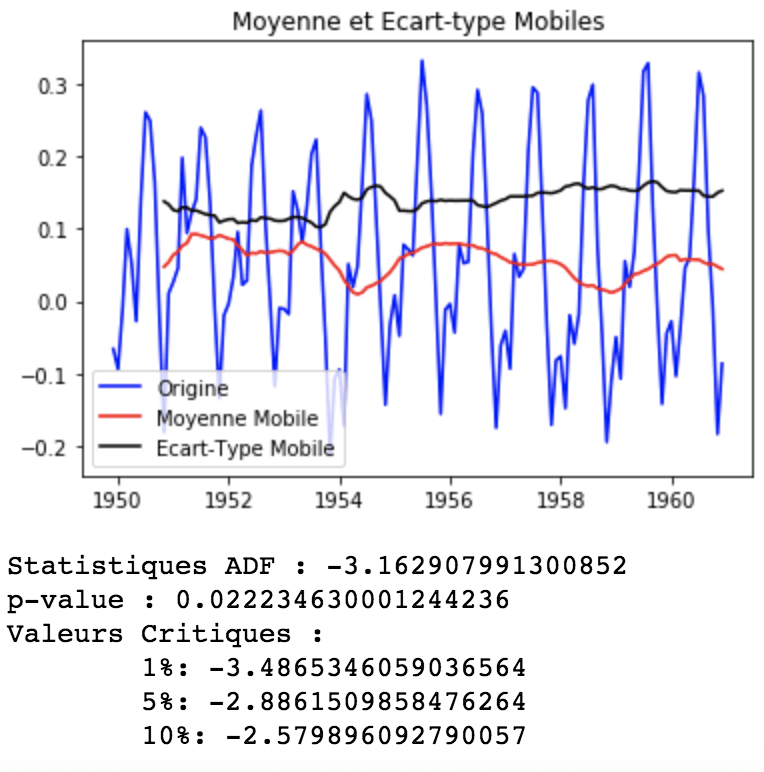
Comme on peut le voir, après soustraction de la moyenne, la moyenne mobile et l’écart-type sont approximativement horizontaux. La p-value est inférieure au seuil de 0,05 et la statistique ADF est proche des valeurs critiques. Par conséquent, la série temporelle est stationnaire.
L’application de la décroissance exponentielle est une autre façon de transformer une série temporelle de manière à ce qu’elle soit stationnaire :
rolling_mean_exp_decay = df_log.ewm(halflife=12, min_periods=0, adjust=True).mean() df_log_exp_decay = df_log - rolling_mean_exp_decay df_log_exp_decay.dropna(inplace=True) get_stationarity(df_log_exp_decay)
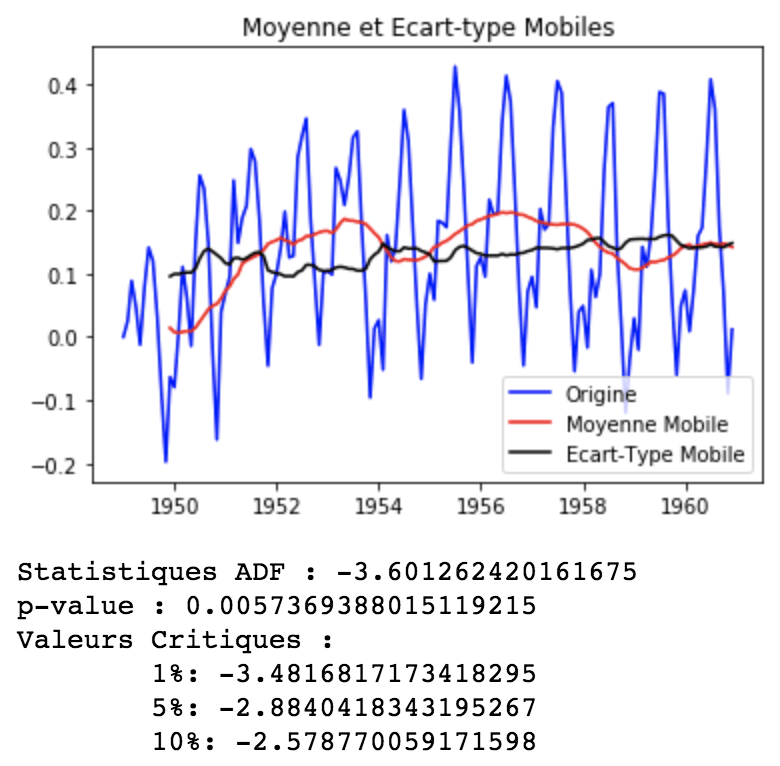
La décroissance exponentielle a été pire que la soustraction de la moyenne mobile. Cependant, elle est plus stationnaire que l’original.
Essayons une autre méthode pour déterminer s’il existe une solution encore meilleure. En appliquant le décalage temporel, nous soustrayons chaque point par celui qui l’a précédé.
null, (x1−x0), (x2−x1), (x3−x2), (x4−x3), …, (xn−xn−1)
df_log_shift = df_log - df_log.shift() df_log_shift.dropna(inplace=True) get_stationarity(df_log_shift)
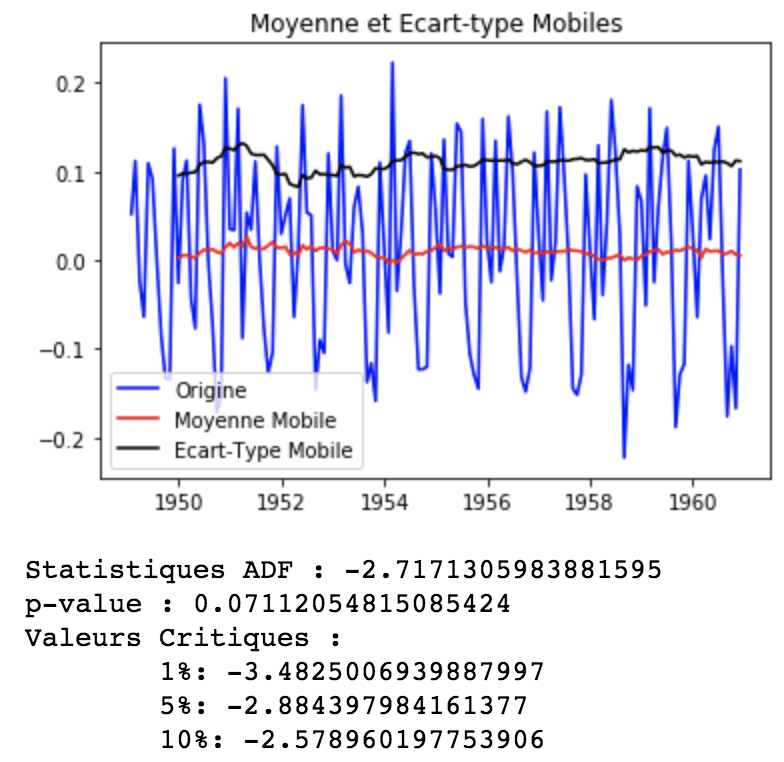
Le décalage temporel est moins bons que la soustraction de la moyenne mobile. Cependant, il est toujours plus stationnaire que l’original.
Modèle Auto-Régressif (AR)
Les modèles auto-régressifs fonctionnent en partant du principe que les valeurs passées ont un effet sur les valeurs actuelles. Les modèles AR sont couramment utilisés pour analyser la nature, l’économie et d’autres processus variables dans le temps. Tant que l’hypothèse tient, nous pouvons construire un modèle de régression linéaire qui tente de prédire aujourd’hui la valeur d’une variable dépendante, compte tenu des valeurs qu’elle avait les jours précédents.
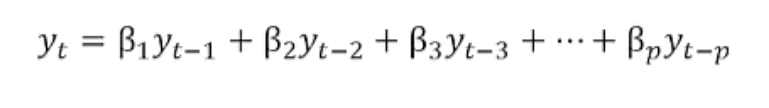
L’ordre du modèle AR correspond au nombre de jours incorporé dans la formule.
Modèle de la Moyenne Mobile (MA)
Supposez que la valeur de la variable dépendante du jour en cours dépend des termes d’erreur des jours précédents. La formule peut être exprimée sous cette forme :
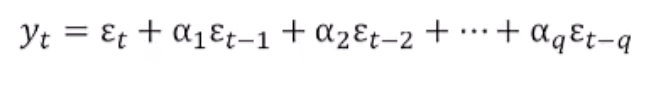
Vous pouvez également tomber sur l’équation écrite comme ceci :
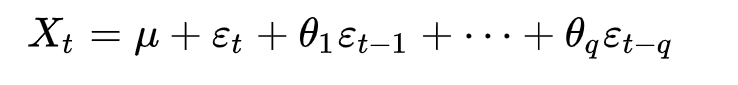
où μ est la moyenne de la série, les θ1, …, θq sont les paramètres du modèle et les εt, εt-1,…, εt-q sont les termes d’erreur de bruit. La valeur de q est appelée l’ordre du modèle MA.
Modèle de la Moyenne Mobile Auto-Régressive (ARMA)
Le modèle ARMA est simplement la combinaison des 2 précédents modèles AR et MA :
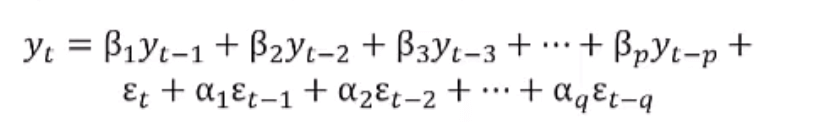
Modèle de la Moyenne Mobile Auto-Régressive Intégrée (ARIMA)
Le modèle ARIMA ajoute une différence à un modèle ARMA. La différenciation soustrait la valeur actuelle de la précédente et peut être utilisée pour transformer une série temporelle en une série stationnaire. Par exemple, la différenciation du premier ordre traite des tendances linéaires et utilise la transformation zi = yi – yi-1. La différenciation du second ordre traite des tendances quadratiques et utilise une différence du premier ordre sur une différence du premier ordre, à savoir zi = (yi – yi-1) – (yi-1 – yi-2), et ainsi de suite.
Trois entiers (p, d, q) sont généralement utilisés pour paramétrer les modèles ARIMA :
- p : nombre de termes autorégressifs (ordre AR)
- d : nombre de différences non saisonnières (ordre de différenciation)
- q : nombre de termes moyens mobiles (ordre MA)
Fonction d’Auto-Corrélation (ACF)
La corrélation entre les observations à l’instant actuel et les observations à tous les instants précédents. Nous pouvons utiliser l’ACF pour déterminer le nombre optimal de termes MA. Le nombre de termes détermine l’ordre du modèle.
Fonction d’Auto-Corrélation Partielle (PACF)
Comme son nom l’indique, le PACF est un sous-ensemble du ACF. Le PACF exprime la corrélation entre les observations faites à deux moments dans le temps tout en tenant compte de l’influence éventuelle d’autres points de données. Nous pouvons utiliser le PACF pour déterminer le nombre optimal de termes à utiliser dans le modèle AR. Le nombre de termes détermine l’ordre du modèle.
Prenons un exemple. Rappelons que le PACF peut être utilisé pour déterminer le meilleur ordre du modèle AR. Les lignes bleues horizontales en pointillé représentent les seuils de signification. Les lignes verticales représentent les valeurs de l’ACF et du PACF à un moment donné. Seules les lignes verticales qui dépassent les lignes horizontales sont considérées comme significatives.
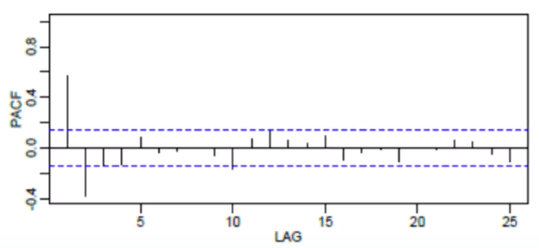
Ainsi, nous utiliserions les deux jours précédents dans l’équation d’Auto-Régression.
Rappelons que l’ACF peut être utilisé pour déterminer le meilleur ordre du modèle MA :
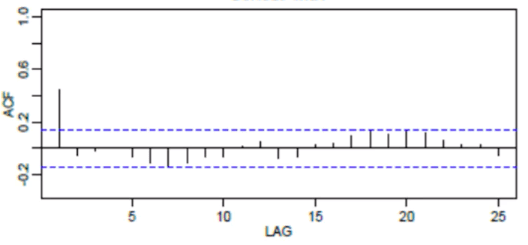
Ainsi, nous n’utilisons que la journée de la veille dans l’équation de la moyenne mobile.
Pour revenir à notre exemple, nous pouvons créer et ajuster un modèle ARIMA avec un AR d’ordre 2, une différence d’ordre 1 et un MA d’ordre 2 :
decomposition = seasonal_decompose(df_log) model = ARIMA(df_log, order=(2,1,2)) results = model.fit(disp=-1) plt.plot(df_log_shift) plt.plot(results.fittedvalues, color='red')
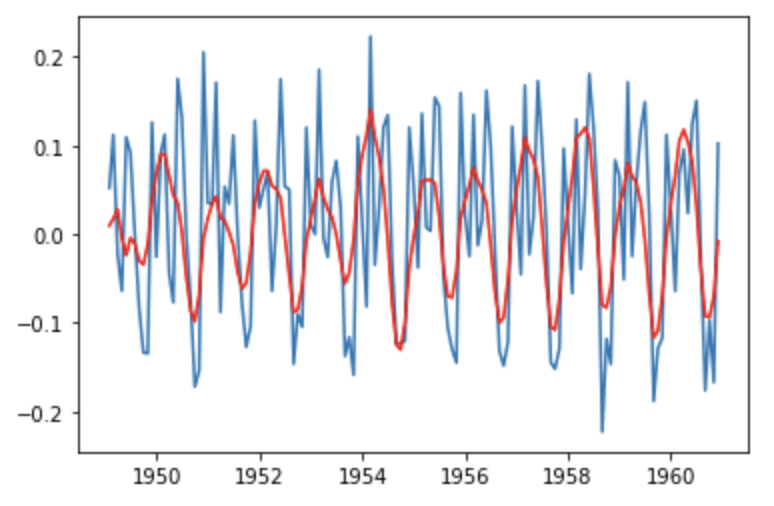
Ensuite, nous pouvons comparer le modèle à la série temporelle d’origine.
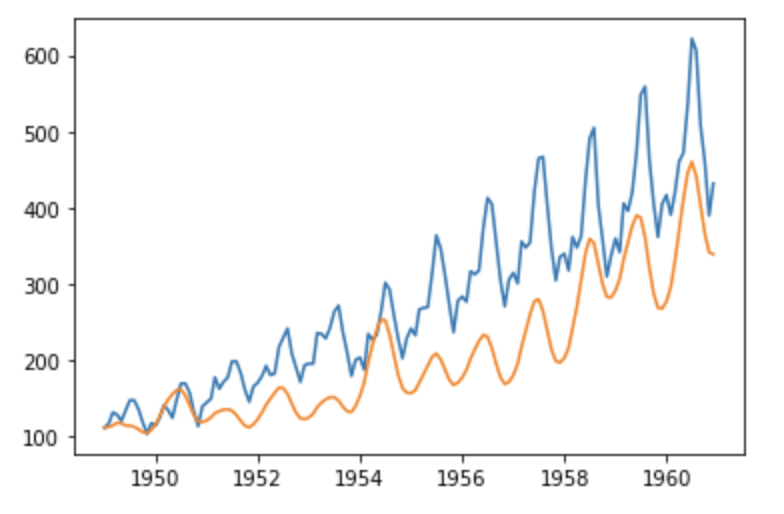
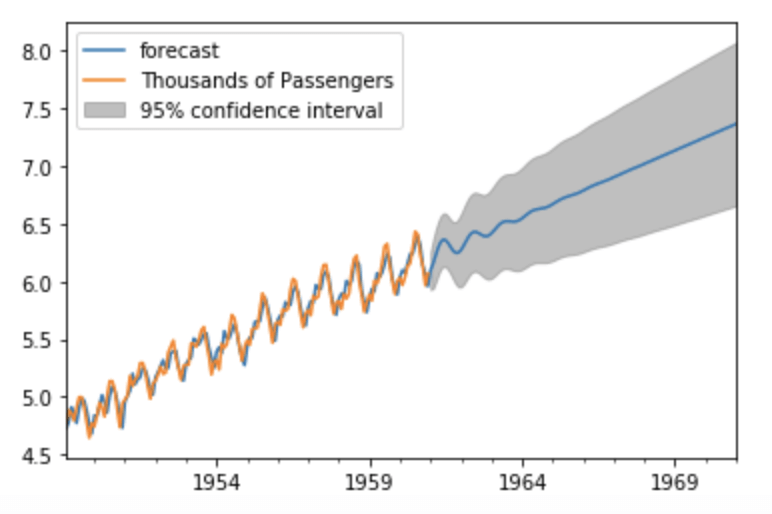
Étant donné que nous disposons de données pour chaque mois remontant à 12 ans et que nous voulons prévoir le nombre de passagers pour les 10 prochaines années, nous utilisons (12 x12)+ (12 x 10) = 264.
fig = results.plot_predict(1,264)
Conclusion
Dans le domaine du Machine Learning, il existe une collection de techniques permettant de manipuler et d’interpréter des variables qui dépendent du temps. Parmi celles-ci, ARIMA peut supprimer la composante de tendance afin de prédire avec précision les valeurs futures.
Pour plus de détails, regardez ma formation complète d’Analyse Financière et de Trading algorithmique.