En tant que data scientist, le Machine Learning c’est un peu notre arsenal pour faire notre travail. Tout expert des données utilise le Machine Learning pour analyser ses données et produire des modèles utiles. Mais alors pourquoi avons-nous besoin d’apprendre les mathématiques du Machine Learning ?
Voici quelques arguments :
- Les mathématiques vous aident à sélectionner le bon algorithme de Machine Learning. La compréhension des mathématiques vous permet donc de mieux comprendre le fonctionnement du modèle, notamment le choix du bon paramètre du modèle et les stratégies de validation.
- L’estimation de la confiance que nous avons dans le résultat du modèle en produisant le bon intervalle de confiance et les mesures d’incertitude nécessite une compréhension des mathématiques.
- Le bon modèle doit prendre en compte de nombreux aspects tels que la metrics, le temps d’apprentissage, la complexité du modèle, le nombre de paramètres et le nombre de features, ce qui nécessite évidemment des mathématiques pour comprendre tous ces aspects.
- Vous pourriez développer un modèle personnalisé adapté à votre propre problème en connaissant les mathématiques qui se cachent derrière les modèles de Machine Learning.
Le principal problème est de savoir de quel domaine mathématique vous avez besoin pour comprendre le Machine Learning. Après tout, les mathématiques sont un vaste domaine…
C’est pourquoi, dans cet article, j’aimerais présenter les domaines ou sujets mathématiques dont vous avez besoin pour le Machine Learning.
Mathématiques du Machine Learning
Nous pouvons donc apprendre de nombreux domaines à partir des mathématiques, mais ici nous voulons nous concentrer sur les mathématiques du Machine Learning, c’est à dire les mathématiques qui se cachent derrière les algorithmes de Machine Learning.
Voici les domaines des mathématiques qui vont nous intéresser. Au menu :

Ces 6 domaines mathématiques constituent la base du Machine Learning. Chaque matière est entrelacée pour développer notre modèle de Machine Learning et atteindre le “meilleur” modèle afin de généraliser l’ensemble de données.
Essayons de développer chaque domaine plus en profondeur pour comprendre de quoi il s’agit.
Algèbre Linéaire
Qu’est-ce que l’algèbre linéaire ? C’est une branche des mathématiques qui concerne l’étude des vecteurs et des règles permettant de manipuler les vecteurs. Lorsque nous formalisons des concepts intuitifs, l’approche commune consiste à construire un ensemble d’objets (symboles) et un ensemble de règles pour manipuler ces objets. C’est ce que nous connaissons sous le nom d’algèbre.
Si nous parlons d’algèbre linéaire dans le Machine Learning, elle est définie comme la partie des mathématiques qui utilise l’espace vectoriel et les matrices pour représenter les équations linéaires.
Lorsque l’on parle de vecteurs, on peut se remémorer l’étude qu’on a faite au lycée sur le vecteur avec la direction (voir l’image ci-dessous).
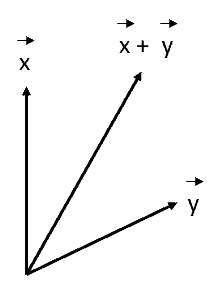
Il s’agit d’un vecteur, mais pas du même type que le vecteur représenté sur l’image suivante.
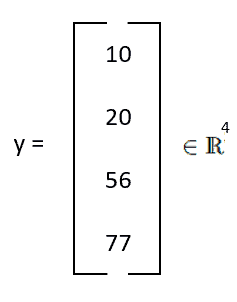
Ce que nous avions ci-dessus est également un vecteur, mais un autre type de vecteur. Vous êtes peut-être familier avec la forme matricielle (l’image ci-dessous). Le vecteur est une matrice avec seulement une colonne, que l’on appelle un vecteur colonne. En d’autres termes, nous pouvons considérer une matrice comme un groupe de vecteurs colonnes ou de vecteurs lignes. En résumé, les vecteurs sont des objets spéciaux qui peuvent être additionnés et multipliés par des scalaires pour produire un autre objet du même type. Nous pouvons avoir différents objets appelés vecteurs.
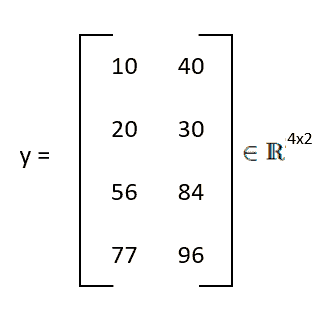
L’algèbre linéaire est une représentation systématique de données que les ordinateurs peuvent comprendre, et toutes les opérations en algèbre linéaire sont des règles systématiques. C’est pourquoi dans le machine Learning moderne, l’algèbre linéaire est une composante importante.
Un exemple de l’utilisation de l’algèbre linéaire est l’équation linéaire. L’algèbre linéaire est un outil utilisé dans l’équation linéaire car de nombreux problèmes peuvent être présentés systématiquement de manière linéaire. L’équation linéaire typique est présentée sous la forme ci-dessous.
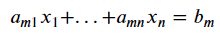
Pour résoudre le problème d’équation linéaire ci-dessus, nous utilisons l’algèbre linéaire pour présenter l’équation linéaire dans une représentation systématique. De cette façon, nous pouvons utiliser la caractérisation matricielle pour rechercher la solution la plus optimale.
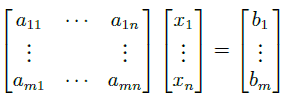
Pour synthétiser le domaine de l’algèbre linéaire, il y a trois éléments que vous devriez connaître parfaitement comme point de départ :
- vecteur
- matrice
- équation linéaire
Géométrie Analytique
La géométrie analytique (ou géométrie des coordonnées) est un domaine dans lequel nous utilisons la position des (points de) données à l’aide d’une paire ordonnée de coordonnées. Ce domaine porte sur la définition et la représentation numérique des formes géométriques et sur l’extraction d’informations quantifiables à partir de ces formes. De façon plus simple, nous projetons des données dans un plan, et puis nous recevons des informations numériques à partir de cela.
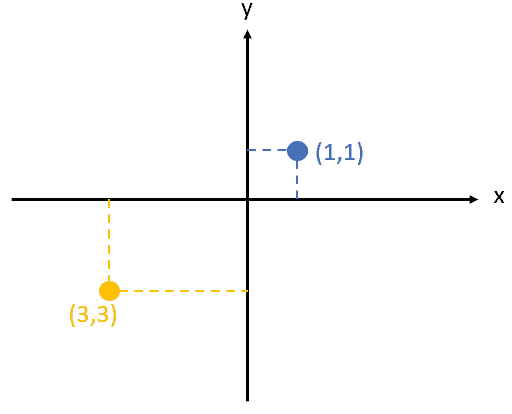
L’exemple ci-dessus montre comment nous avons obtenu des informations à partir du point de données en projetant l’ensemble des données dans le plan. La façon dont nous acquérons les informations à partir de cette représentation est le cœur de la géométrie analytique. Pour vous aider à commencer à apprendre ce sujet, voici quelques termes importants dont vous pourriez avoir besoin.
Fonction distance
Une fonction distance est une fonction qui fournit des informations numériques sur la distance entre les éléments d’un ensemble. Si la distance est nulle, alors les éléments sont équivalents. Dans le cas contraire, ils sont différents les uns des autres.
Un exemple de fonction distance est la distance euclidienne qui calcule la distance linéaire entre deux points de données.
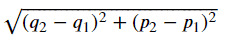
Produit scalaire
Le produit scalaire est un concept qui introduit des notions géométriques intuitives, telles que la longueur d’un vecteur et l’angle ou la distance entre deux vecteurs. Il est souvent noté ⟨x,y⟩ (ou parfois (x,y) ou ⟨x|y⟩).
Décomposition matricielle
La décomposition matricielle est le domaine qui concerne la manière de réduire une matrice. La décomposition matricielle vise à simplifier les opérations matricielles plus complexes sur la matrice décomposée plutôt que sur sa matrice d’origine.
Une analogie courante pour la décomposition matricielle est la factorisation de nombres, comme la factorisation de 8 en 2 x 4. C’est pourquoi la décomposition matricielle est synonyme de factorisation de matrice. Il existe de nombreuses façons de décomposer une matrice, et donc un ensemble de techniques de décomposition matricielle varié.
Un exemple est la décomposition LU ci-dessous. Il s’agit d’une méthode de décomposition d’une matrice comme produit d’une matrice triangulaire inférieure L (comme lower, inférieure en anglais) par une matrice triangulaire supérieure U (comme upper, supérieure).
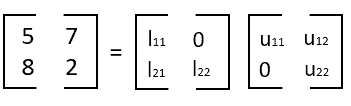
Calcul vectoriel
Le calcul est un domaine mathématique qui concerne la variation continue, qui consiste principalement en des fonctions et des limites. Le calcul vectoriel lui-même s’intéresse à la différenciation et à l’intégration des champs vectoriels. Le calcul vectoriel est souvent appelé calcul multivarié, bien que son cas d’étude soit légèrement différent. Le calcul multivarié traite des fonctions d’application du calcul des multiples variables indépendantes.
Il y a quelques termes importants que vous devez connaître lorsque vous commencez à apprendre le calcul vectoriel :
Dérivée et différentiation
La dérivée est une fonction de nombres réels qui mesure la variation de la valeur de la fonction (valeur de sortie) concernant une variation de son argument (valeur d’entrée).
La différentiation est l’action de calculer une dérivée.

Dérivée partielle
La dérivée partielle est une fonction dérivée où plusieurs variables sont calculées à l’intérieur de la fonction dérivée par rapport à l’une de ces variables qui peut varier, sachant que les autres variables sont maintenues constantes (par opposition à la dérivée totale, dans laquelle toutes les variables peuvent varier).
Gradient
Le gradient est un mot lié à la dérivée ou au taux de variation d’une fonction (vous pourriez considérer le gradient comme est un mot fantaisiste pour dérivée). Le terme gradient est généralement utilisé pour les fonctions ayant plusieurs entrées et une seule sortie (scalaire). Le gradient a une direction pour se déplacer à partir de son emplacement actuel, par exemple, vers le haut, le bas, la droite, la gauche…
Probabilité et Distributions
La probabilité est l’étude de l’incertitude (au sens large). La probabilité peut être considérée ici comme le moment où l’événement se produit ou le degré de croyance de l’occurrence d’un événement. La distribution de probabilité est une fonction qui mesure la probabilité d’un résultat particulier (ou d’un ensemble de résultats) qui se produirait, associé à la variable aléatoire. La fonction de distribution de probabilité courante est illustrée dans l’image ci-dessous.
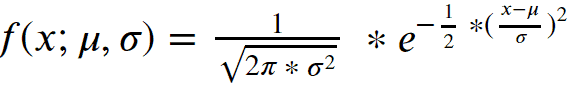
La théorie des probabilités et les statistiques sont souvent associées à une chose similaire, mais elles concernent des aspects différents de l’incertitude :
- En mathématiques, nous définissons la probabilité comme un modèle où les variables aléatoires capturent l’incertitude sous-jacente, et nous utilisons les règles de probabilité pour résumer ce qui se passe.
- En statistiques, nous essayons de comprendre le processus sous-jacent qui observe quelque chose qui s’est produit et tente d’expliquer les observations.
Lorsque l’on parle de Machine Learning, il est proche des statistiques car son objectif est de construire un modèle qui représente de manière adéquate le processus qui a généré les données.
Optimisation
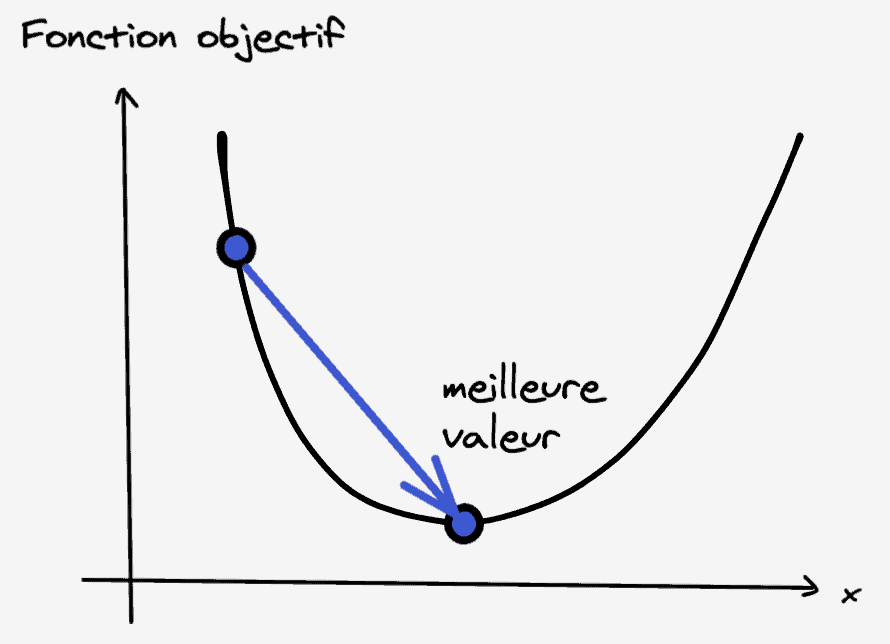
Dans l’objectif d’apprentissage, l’entraînement d’un modèle de Machine Learning consiste à trouver un bon ensemble de paramètres. Ce que nous considérons comme “bon” est déterminé par la “fonction objectif” ou les modèles probabilistes. C’est à cela que servent les algorithmes d’optimisation (étant donné une fonction objectif, nous essayons de trouver la meilleure valeur).
En général, les fonctions objectifs dans le Machine Learning essaient de minimiser la fonction. Cela signifie que la meilleure valeur est la valeur minimale. Intuitivement, si nous essayons de trouver la meilleure valeur, cela reviendrait à trouver les vallées de la fonction objectif là où les gradients nous font remonter. C’est pourquoi nous voulons nous déplacer en descendant (à l’opposé du gradient) et espérer trouver le point le plus bas (le plus profond). C’est le concept de descente de gradient.
Il existe quelques termes à connaître pour apprendre l’optimisation :
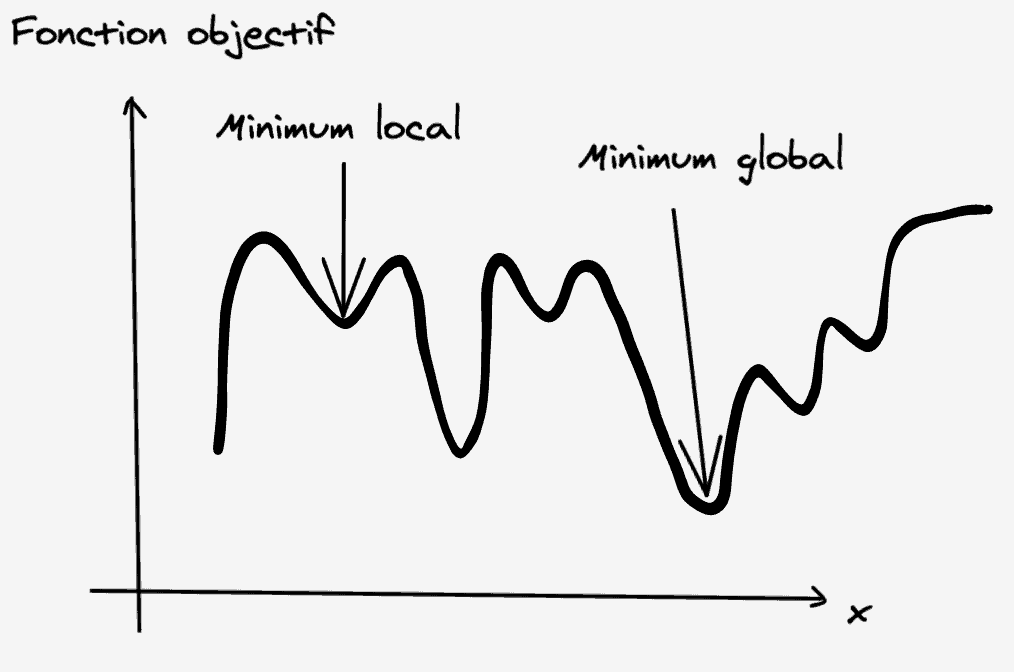
Minima locaux et minima globaux
Le point où une fonction prend la valeur minimale est appelé le minimum global. Cependant, lorsque l’objectif est de minimiser la fonction et de la résoudre à l’aide d’algorithmes d’optimisation tels que la descente de gradient, la fonction pourrait avoir une valeur minimale en différents points. Ces différents points qui semblent être des minima mais qui ne sont pas le point où la fonction prend réellement la valeur minimale sont appelés des minima locaux.
Optimisation sans contrainte et optimisation avec contrainte
L’optimisation sans contrainte est une fonction d’optimisation dans laquelle nous trouvons le minimum d’une fonction en supposant que les paramètres peuvent prendre n’importe quelle valeur possible (aucune limitation des paramètres). L’optimisation avec contraintes limite simplement la valeur possible en introduisant un ensemble de contraintes.
La descente de gradient est une optimisation sans contrainte s’il n’y a pas de limitation des paramètres. Si nous fixons une certaine limite, par exemple, x > 1, il s’agit d’une optimisation sans contrainte.
Conclusion
Le Machine Learning est un outil quotidien que les spécialistes des données ou data scientists utilisent pour obtenir de précieux modèles dont nous avons besoin. Apprendre les mathématiques du Machine Learning peut vous donner un réel avantage dans votre travail. Il existe de nombreux domaines mathématiques, mais il y a 6 domaines qui comptent le plus lorsque nous commençons à apprendre les mathématiques du Machine Learning, qui sont :
- Algèbre Linéaire
- Géométrie Analytique
- Décomposition Matricielle
- Calcul Vectoriel
- Probabilité et Distributions
- Optimisation











Merci pour cet article qui est super instructif.
Ravi qu’il te plaise 🙂