La curiosité et l’intuition sont deux des outils les plus puissants du Data Scientist. Le troisième est peut-être le Pandas…
Nous allons voir ici l’extraction d’informations avec Pandas et Seaborn, en utilisant un dataset Kaggle.
Dans un précédent article, je vous ai montré comment avoir une idée du degré d’exhaustivité d’un ensemble de données, tracer quelques variables et examiner les tendances et les évolutions dans le temps.
Pour ce faire, nous avons utilisé le DataFrame Pandas de Python sur un Notebook Jupyter pour l’analyse et le traitement des données, et le Framework Seaborn pour les visuels.
Pour l’article précédent, comme pour celui-ci, nous avons utilisé l’ensemble de données de Kaggle “120 ans d’histoire olympique: athlètes et résultats” que vous pouvez télécharger ici. Et nous avons examiné la participation des femmes au fil du temps, la répartition du poids et de la taille des athlètes, ainsi que d’autres variables, mais nous n’avons pas utilisé les données sur le sport que chaque athlète pratiquait.
Cette fois-ci, nous nous concentrerons sur la colonne Sport de la base de données pour en tirer quelques enseignements.
Voici quelques questions auxquelles on peux penser :
- Quels sont les sports qui favorisent les gens costauds ? Qu’en est-il des personnes de grande taille ?
- Quels sont les sports les plus récents et les plus anciens ? Y a-t-il des sports qui ont réellement perdu la faveur des Jeux olympiques et qui ont cessé d’être pratiqués ?
- Y a-t-il des sports où les mêmes équipes gagnent toujours ? Qu’en est-il des sports les plus divers, dont les vainqueurs viennent de nombreux endroits différents ?
Comme précédemment, voici le notebook de l’analyse des sports du code ci-dessous.
Plongeons dans le vif du sujet !
Poids et Taille
Pour notre première analyse, nous allons examiner quels sports ont les joueurs les plus lourds et les plus grands, et quels sont ceux qui ont les plus légers ou les plus petits.
Comme nous l’avons vu dans l’article précédent, la taille et le poids dépendent fortement du sexe, et nous disposons de plus de données sur les athlètes masculins que sur les athlètes féminines. Nous allons donc faire cette analyse sur les hommes, mais le même code fonctionnerait pour les deux en changeant simplement le filtre “Sex”.
male_df = df[df.Sex=='M']
sport_weight_height_metrics = male_df.groupby(['Sport'])['Weight','Height'].agg(
['min','max','mean'])
sport_weight_height_metrics.Weight.dropna().sort_values('mean', ascending=False)[:5]
Comme vous pouvez le voir, si je regroupe par sport, je peux prendre le poids et la taille minimum, maximum et moyenne pour les joueurs de chaque sport.
J’ai ensuite regardé les 5 sports avec les athlètes les plus lourds et j’ai trouvé ceci (en kilogrammes) :
Sport min max average Tug-Of-War 75.0 118.0 95.61 Basketball 59.0 156.0 91.68 Rugby Sevens 65.0 113.0 91.00 Bobsleigh 55.0 145.0 90.38 Beach Volleyball 62.0 110.0 89.51
Rien d’inattendu, n’est-ce pas ? Les tireurs à la corde, les joueurs de basket-ball et de rugby sont tous lourds. Il est assez intéressant de voir qu’il y a tant de variations chez les joueurs de basket-ball et de rugby, passant de 59 à 156 kg, alors que la plupart des tireurs à la corde pèsent plus de 80 kilos.
Ensuite, j’ai simplement tracé le poids moyen pour chaque sport, et j’ai constaté qu’il y avait une répartition assez normale :
sns.distplot(sport_weight_height_metrics.Weight.dropna()['mean'])
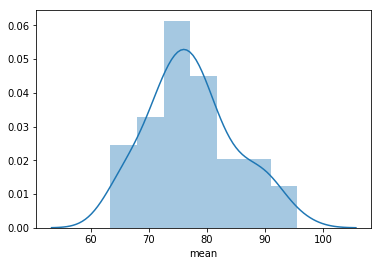
La taille des athlètes a une distribution normale similaire, mais sa variance est beaucoup plus faible, étant fortement concentrée dans la moyenne :
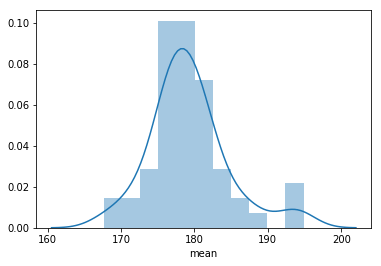
Ensuite, j’ai représenté graphiquement toutes les moyennes individuels, dans un diagramme de dispersion ordonné, pour voir s’il n’y avait pas de valeurs aberrantes.
means = list(sport_weight_height_metrics.Weight.dropna()['mean'])
sports = list(sport_weight_height_metrics.Weight.dropna().index)
plot_data = sorted(zip(sports, means), key = lambda x:x[1])
plot_data_dict = {
'x' : [i for i, _ in enumerate(plot_data)],
'y' : [v[1] for i, v in enumerate(plot_data)],
'group' : [v[0] for i, v in enumerate(plot_data)]
}
sns.scatterplot(data = plot_data_dict, x = 'x' , y = 'y')
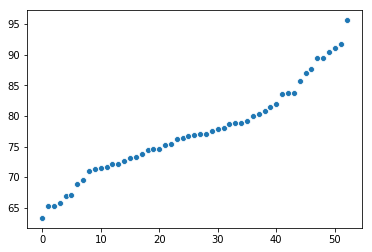
En fait, le sport le plus “lourd” est tout à fait en dehors du reste du graphique, et il en va de même pour le plus “léger”. Si l’on regarde les hauteurs, même si la variance était nettement plus faible, le graphique révèle une différence encore plus grande entre les “valeurs aberrantes” et les personnes proches de la moyenne, accentuée par le fait que la plupart des personnes ne s’en écartent pas vraiment.
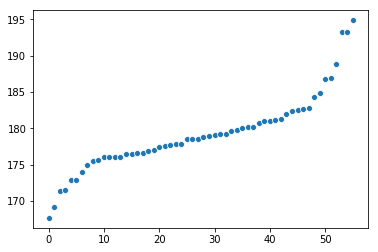
Pour les sports les plus légers, les résultats peuvent être obtenus en utilisant la variable précédemment générée, plot_data.
print('lightest:')
for sport,weight in plot_data[:5]:
print(sport + ': ' + str(weight))
print('\nheaviest:')
for sport,weight in plot_data[-5:]:
print(sport + ': ' + str(weight))
Les résultats (en omettant les plus lourds, puisque nous les avons déjà vus) sont les suivants :
lightest: Gymnastics: 63.3436047592 Ski Jumping: 65.2458805355 Boxing: 65.2962797951 Trampolining: 65.8378378378 Nordic Combined: 66.9095595127
Ainsi, les athlètes de gymnastique, même masculins, sont de loin les plus légers ! Ils sont suivis de près par le saut à ski, la boxe (ce qui m’a un peu surpris, puisqu’il y a différentes catégories de boxeurs) et le trampoline, ce qui est en fait très logique.
Si nous recherchons plutôt les athlètes les plus grands et les plus petits, les résultats seront un peu moins surprenants. Je suppose que nous nous attendions tous à ce que le même sport arrive en tête et, sans surprise, c’est ce qui s’est passé. Au moins, nous pouvons maintenant dire que ce n’est pas un stéréotype.
shortest (cm): Gymnastics: 167.644438396 Weightlifting: 169.153061224 Trampolining: 171.368421053 Diving: 171.555352242 Wrestling: 172.870686236 tallest (cm): Rowing: 186.882697947 Handball: 188.778373113 Volleyball: 193.265659955 Beach Volleyball: 193.290909091 Basketball: 194.872623574
On voit donc que les pratiquants de gymnastique sont très légers, et très petite. Mais certains sports de ces classements n’apparaissent pas dans les poids. Je me demande quelle est la “corpulence” (poids/taille) de chaque sport ?
mean_heights = sport_weight_height_metrics.Height.dropna()['mean']
mean_weights = sport_weight_height_metrics.Weight.dropna()['mean']
avg_build = mean_weights/mean_heights
avg_build.sort_values(ascending = True)
builds = list(avg_build.sort_values(ascending = True))
plot_dict = {'x':[i for i,_ in enumerate(builds)],'y':builds}
sns.lineplot(data=plot_dict, x='x', y='y')
Le tracé a un aspect assez linéaire, jusqu’à ce que nous arrivions au sommet où la plupart des valeurs aberrantes tombent :
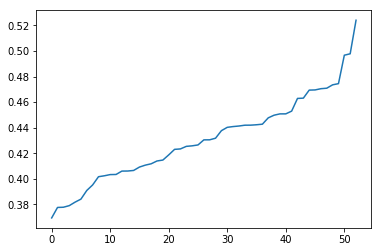
Et voici les sports les moins et les plus “trapus” (répartition poids/taille) :
Smallest Build (Kg/centimeters) Alpine Skiing 0.441989 Archery 0.431801 Art Competitions 0.430488 Athletics 0.410746 Badminton 0.413997 Heaviest Build Tug-Of-War 0.523977 Rugby Sevens 0.497754 Bobsleigh 0.496656 Weightlifting 0.474433 Handball 0.473507
Une fois encore, le rugby et le tir à la corde sont les sports où les athlètes sont les plus développés, et cette fois-ci, le ski alpin est le moins développé, suivi de près par le tir à l’arc et les compétitions artistiques (qui nécessitera des recherches plus approfondies).
Les sports au cours du temps
Maintenant que nous avons fait toutes les choses intéressantes auxquelles je pouvais penser avec ces trois colonnes, j’aimerais commencer à examiner la variable temporelle. Plus précisément l’année. Je veux voir si de nouveaux sports ont été introduits aux Jeux olympiques, et quand. Mais aussi quels sports ont été délaissés.
Ce code sera généralement utile chaque fois que nous aurons besoin de voir quand quelque chose s’est produit pour la première fois, surtout si nous voulons voir une augmentation anormale d’une variable.
from collections import Counter
sport_min_year = male_df.groupby('Sport').Year.agg(['min','max'])['min'].sort_values('index')
year_count = Counter(sport_min_year)
year = list(year_count.keys())
new_sports = list(year_count.values())
data = {'x':year, 'y':new_sports}
sns.scatterplot(data=data, x = 'x', y='y')
Le graphique nous montre combien de sports ont été pratiqués aux Jeux olympiques pour la première fois chaque année. Ou, en d’autres termes, combien de sports ont été introduits chaque année :

Ainsi, même si beaucoup de sports étaient pratiqués avant 1910 et que la plupart ont été introduits avant 1920, il y a eu beaucoup d’introductions de sports relativement nouvelles. En examinant les données, je constate que de nombreux nouveaux sports ont été introduits en 1936, et qu’ensuite, ils ont toujours été introduits en petits ensembles (moins de cinq sports).
Il n’y a pas eu de nouveaux sports entre 1936 et 1960, lorsque le biathlon a été introduit, et ensuite ils ont continué à en ajouter assez régulièrement :
Sport introduced Biathlon 1960 Luge 1964 Volleyball 1964 Judo 1964 Table Tennis 1988 Baseball 1992 Short Track Speed Skating 1992 Badminton 1992 Freestyle Skiing 1992 Beach Volleyball 1996 Snowboarding 1998 Taekwondo 2000 Trampolining 2000 Triathlon 2000 Rugby Sevens 2016
Une analyse analogue pour les sports dépréciés (où l’année maximale n’est pas récente) montre cette liste de sports, dont la plupart ne m’ont jamais été présentés (bien que ce ne soit en aucun cas une bonne mesure de la popularité d’un sport !)
Basque Pelota 1900 Croquet 1900 Cricket 1900 Roque 1904 Jeu De Paume 1908 Racquets 1908 Motorboating 1908 Lacrosse 1908 Tug-Of-War 1920 Rugby 1924 Military Ski Patrol 1924 Polo 1936 Aeronautics 1936 Alpinism 1936 Art Competitions 1948
On voit que les concours artistiques ont été abandonnés en 1948, que le polo n’est plus pratiqué aux Jeux olympiques depuis 1936, et qu’il en va de même pour l’aéronautique. Si quelqu’un sait ce qu’est exactement la discipline “aéronautique”, qu’il me le fasse savoir. J’imagine des gens dans un avion mais je ne vois pas ce que pourrait être la compétition. Peut-être des courses d’avions ? Dites-moi !
C’est tout pour cette analyse ! J’espère que vous avez apprécié ce tutoriel, et que vous avez peut-être appris un fait intéressant à évoquer lors de votre prochain dîner de famille 🙂
Comme d’habitude, n’hésitez pas à tourner et retourner le code de cette analyse et à y ajouter vos propres idées.