La régression linéaire est généralement le premier algorithme de Machine Learning rencontré par tous les data scientists. Il s’agit d’un modèle simple, mais que tout le monde doit maîtriser car il jette les bases pour d’autres algorithmes de Machine Learning.
Dans quelle situation peut-on utiliser la régression linéaire ?
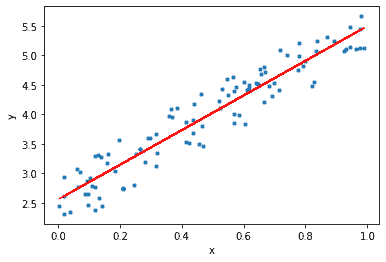
C’est une technique très puissante qui peut être utilisée pour comprendre les facteurs qui influencent la rentabilité. Elle peut être utilisée pour prévoir les ventes des mois à venir en analysant les données de ventes des mois précédents. Elle peut également être utilisée pour obtenir diverses informations sur le comportement des clients. À la fin de cet article, nous allons construire un modèle qui ressemble à l’image ci-dessous, c’est-à-dire déterminer une ligne ou une droite qui correspond le mieux à nos données.
Qu’est-ce que la régression linéaire ?
L’objectif d’un modèle de régression linéaire est de trouver une relation entre une ou plusieurs entités (variables indépendantes) et une variable cible continue (variable dépendante). Lorsqu’il n’y a qu’une entité, elle est appelée Régression linéaire à une variable et s’il existe plusieurs entités, elle est appelée Régression linéaire multiple.
Hypothèse de régression linéaire
Le modèle de régression linéaire peut être représenté par l’équation suivante :
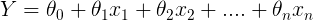
- Y est la valeur prédite
- θ est le terme de biais.
- θ,…, θ sont les paramètres du modèle
- x, x ₂,…, x sont les valeurs des entités.
L’hypothèse ci-dessus peut également être représentée par :
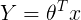
où
- θ est le vecteur de paramètres du modèle, y compris le terme de biais θ
- x est le vecteur d’entités avec x =1
Les données utilisées pour effectuer notre régression linéaire
Créons un ensemble de données aléatoire pour entraîner notre modèle :
# importations
import numpy as np
import matplotlib.pyplot as plt
# générer un dataset aléatoire
np.random.seed(0)
x = np.random.rand(100, 1)
y = 2 + 3 * x + np.random.rand(100, 1)
# tracer le graphique
plt.scatter(x,y,s=10)
plt.xlabel('x')
plt.ylabel('y')
plt.show()
Le graphique de l’ensemble de données généré à l’aide du code ci-dessus est présenté ci-dessous :
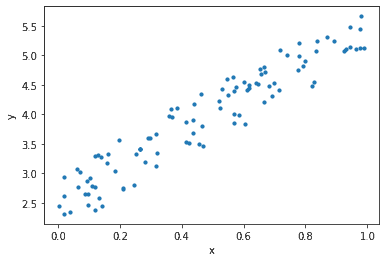
Entraîner un modèle de régression linéaire
Entraîner le modèle ici signifie trouver les paramètres afin que le modèle s’ajuste le mieux aux données.
Comment déterminer la droite qui convient le mieux ?
La droite pour laquelle l’erreur entre les valeurs prévues et les valeurs observées est minimale est appelée droite de meilleure ajustement ou droite de régression. Ces erreurs sont également appelées valeurs résiduelles. Les valeurs résiduelles peuvent être visualisées par les lignes verticales allant de la valeur de données observée à la droite de régression.
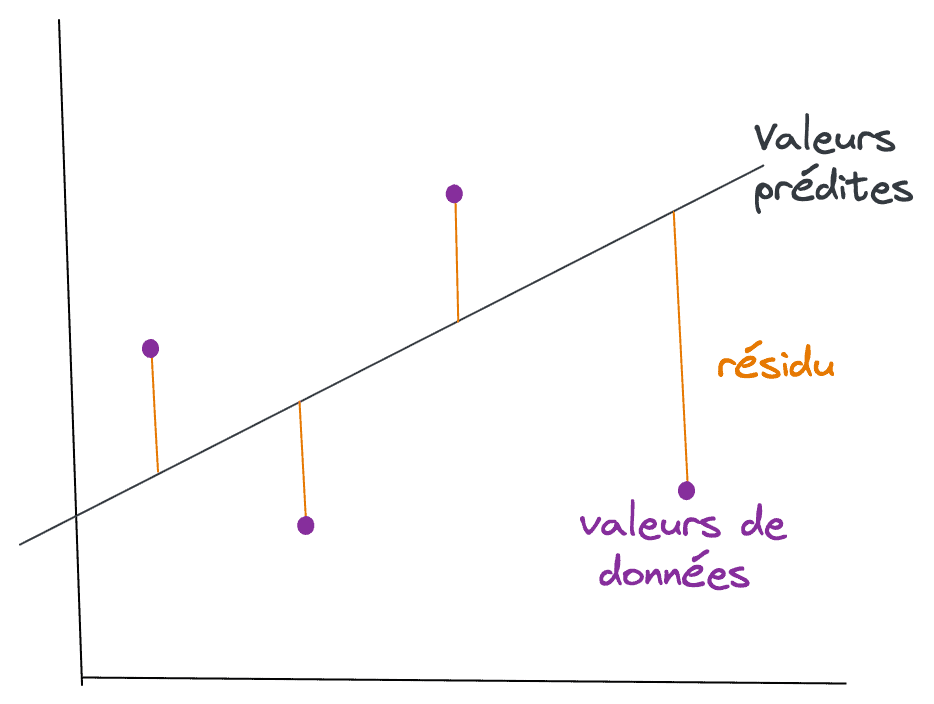
Pour définir et mesurer l’erreur de notre modèle, nous définissons la fonction de coût comme la somme des carrés des valeurs résiduelles.
La fonction de coût est notée par :
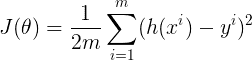
où la fonction d’hypothèse h (x) est désignée par :
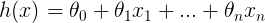
et m représente le nombre total d’exemples d’entraînement dans notre ensemble de données.
Pourquoi prenons-nous le carré des valeurs résiduelles et non la valeur absolue des valeurs résiduelles ?
Parce que nous voulons pénaliser plus fortement les points qui sont plus éloignés de la droite de régression que les points proches de la droite.
Notre objectif est de trouver les paramètres du modèle de manière à ce que la fonction de coût soit minimale. Nous allons utiliser la descente de gradient pour trouver cela.
Descente de Gradient
La descente de gradient est un algorithme d’optimisation générique utilisé dans de nombreux algorithmes de Machine Learning. elle modifie de manière itérative les paramètres du modèle afin de minimiser la fonction de coût. Les étapes de la descente de gradient sont décrites ci-dessous.Nous commençons par initialiser les paramètres du modèle avec des valeurs aléatoires. C’est ce qu’on appelle aussi l’initialisation aléatoire
1/ Nous devons maintenant mesurer l’évolution de la fonction de coût en fonction de l’évolution de ses paramètres
2/ Par conséquent, nous calculons les dérivées partielles de la fonction de coût par rapport aux paramètres θ₀, θ₁, … , θₙ
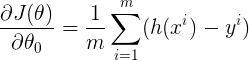
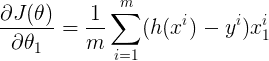
De même, la dérivée partielle de la fonction de coût par rapport à n’importe quel paramètre peut être notée par :
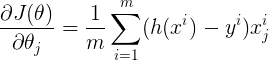
Nous pouvons calculer les dérivées partielles de tous les paramètres à la fois en utilisant :
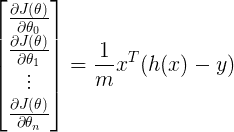
où h (x) est :
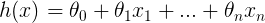
3/ Après le calcul de la dérivée, nous mettons à jour les paramètres comme indiqué ci-dessous
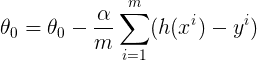
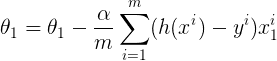
où α est le paramètre d’apprentissage.
Nous pouvons mettre à jour tous les paramètres en une seule fois en utilisant,
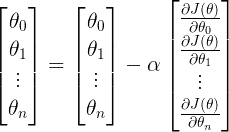
Nous répétons les étapes 2,3 jusqu’à ce que la fonction de coût converge vers la valeur minimale. Si la valeur de α est trop petite, la convergence de la fonction de coût prendra plus de temps. Si α est trop grand, la descente de gradient pourrait dépasser le minimum et finalement échouer à converger.
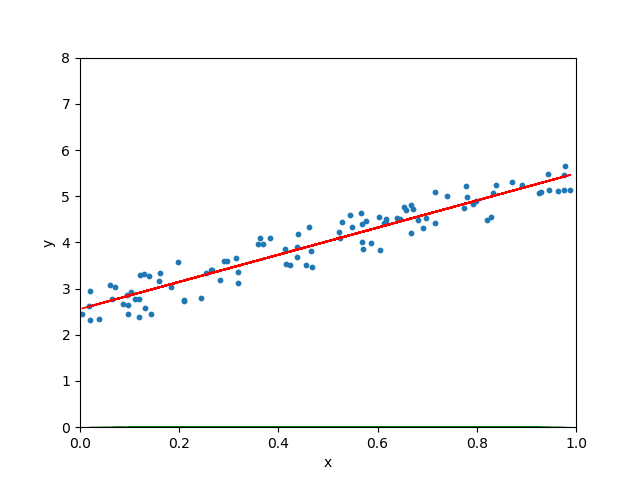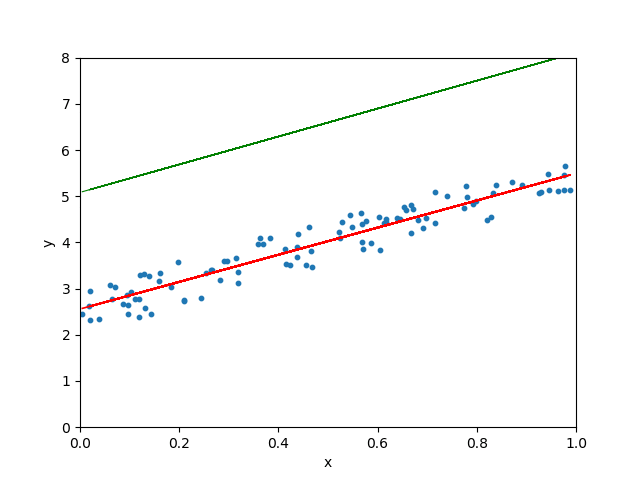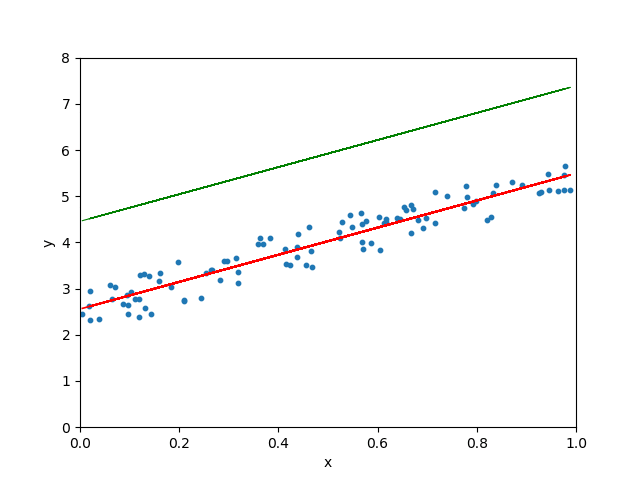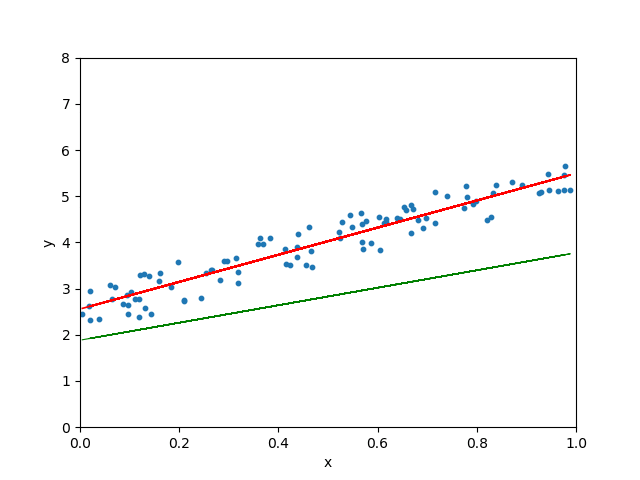
Pour illustrer l’algorithme de descente de gradient, nous initialisons les paramètres du modèle avec 0. L’équation devient Y = 0. L’algorithme de descente de gradient essaie maintenant de mettre à jour la valeur des paramètres afin d’arriver à la meilleure droite d’ajustement.
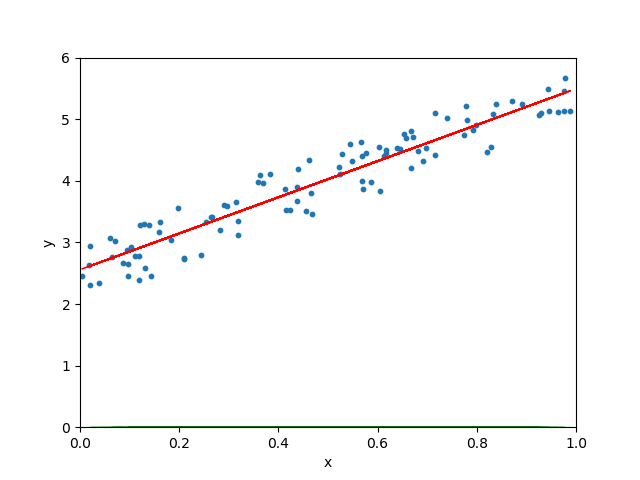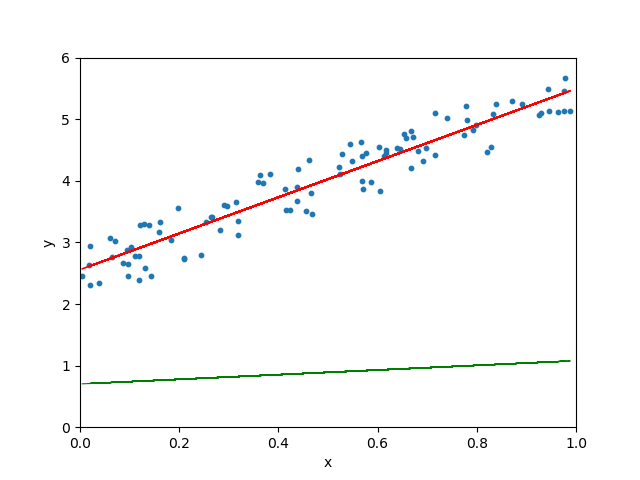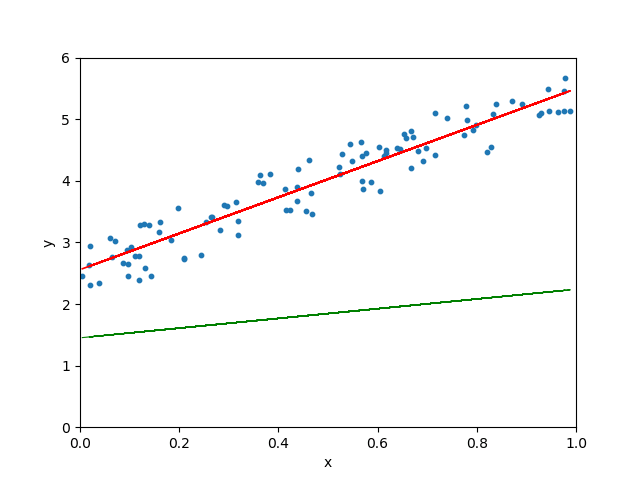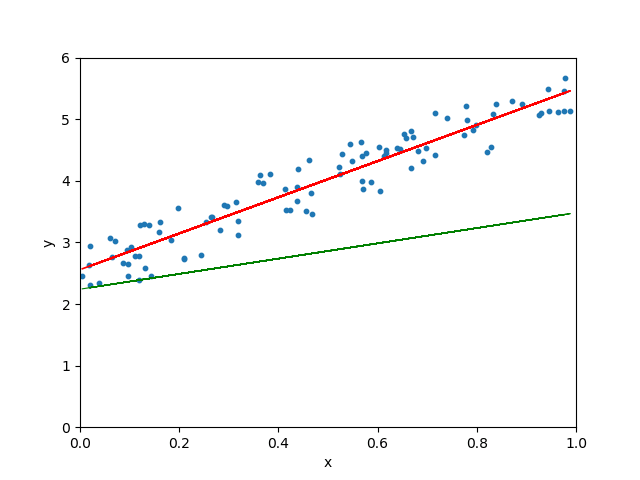
Lorsque le taux d’apprentissage est très lent, la descente de gradient prendra plus de temps pour trouver la droite la mieux adaptée :
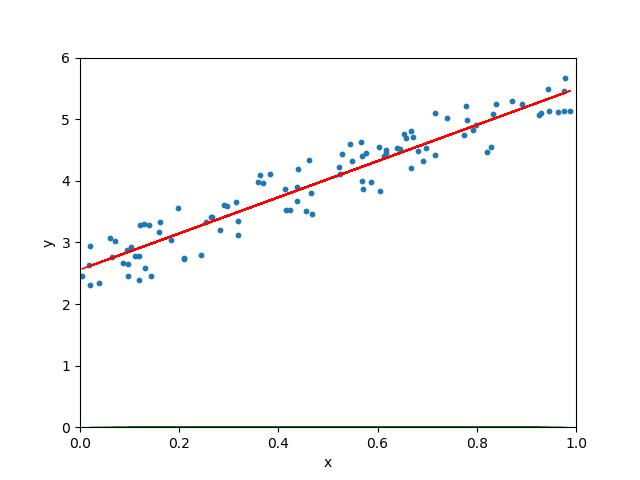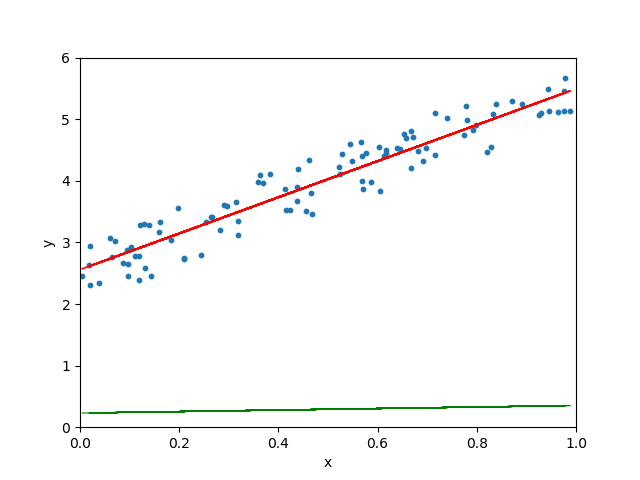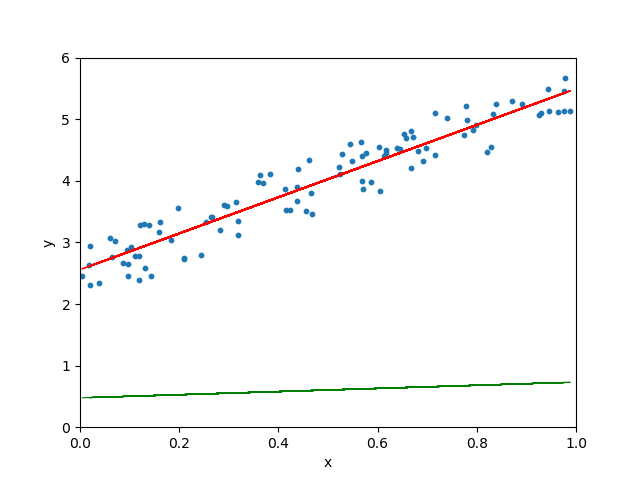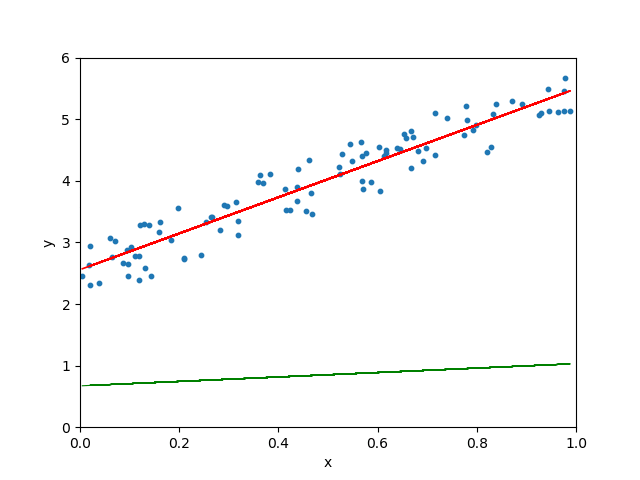
Quand le taux d’apprentissage est normal :
Lorsque le taux d’apprentissage est arbitrairement élevé, l’algorithme de descente de gradient continue de dépasser la droite la mieux ajustée et peut même ne pas trouver la meilleure droite :
Coder une régression linéaire from scratch
L’implémentation complète de la régression linéaire avec descente de gradient est présentée ci-dessous :
import numpy as np
class LinearRegressionUsingGD:
"""Linear Regression Using Gradient Descent.
Parameters
----------
eta : float
Learning rate
n_iterations : int
No of passes over the training set
Attributes
----------
w_ : weights/ after fitting the model
cost_ : total error of the model after each iteration
"""
def __init__(self, eta=0.05, n_iterations=1000):
self.eta = eta
self.n_iterations = n_iterations
def fit(self, x, y):
"""Fit the training data
Parameters
----------
x : array-like, shape = [n_samples, n_features]
Training samples
y : array-like, shape = [n_samples, n_target_values]
Target values
Returns
-------
self : object
"""
self.cost_ = []
self.w_ = np.zeros((x.shape[1], 1))
m = x.shape[0]
for _ in range(self.n_iterations):
y_pred = np.dot(x, self.w_)
residuals = y_pred - y
gradient_vector = np.dot(x.T, residuals)
self.w_ -= (self.eta / m) * gradient_vector
cost = np.sum((residuals ** 2)) / (2 * m)
self.cost_.append(cost)
return self
def predict(self, x):
""" Predicts the value after the model has been trained.
Parameters
----------
x : array-like, shape = [n_samples, n_features]
Test samples
Returns
-------
Predicted value
"""
return np.dot(x, self.w_)
Les paramètres du modèle sont donnés ci-dessous :
Le coefficient est de [2.89114079]. L'ordonnée à l'origine est [2.58109277].
Le tracé de la droite de meilleur ajustement est le suivant :
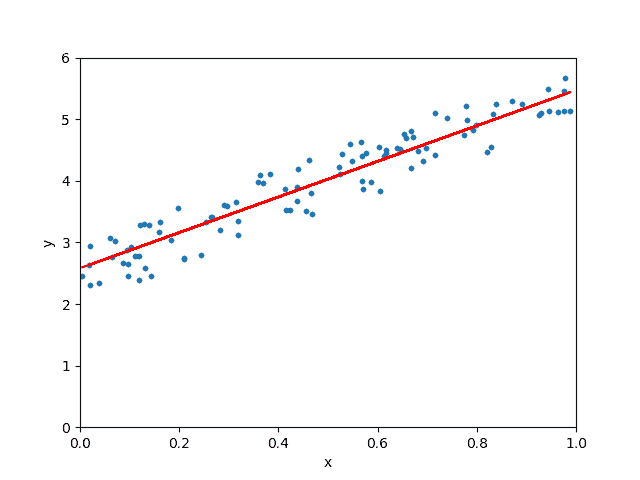
Le graphique de la fonction de coût en fonction du nombre d’itérations est donné ci-dessous. Nous pouvons observer que la fonction de coût diminue à chaque itération au départ et qu’elle converge finalement après près de 100 itérations.
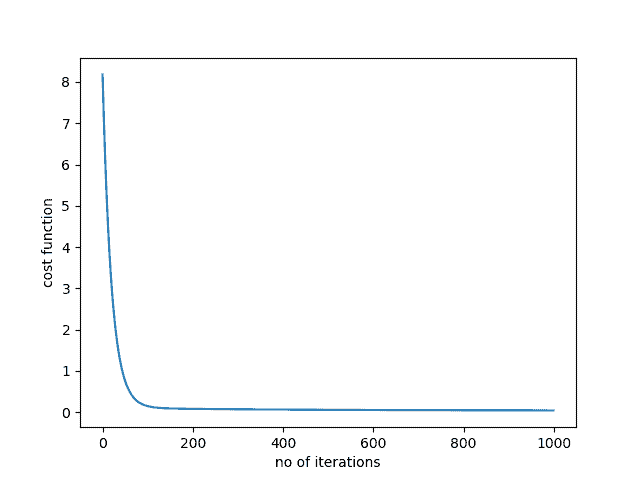
Jusqu’à présent, nous avons implémenté une régression linéaire from scratch (à partir de zéro) et utilisé la descente de gradient pour trouver les paramètres du modèle.
Mais quelle est la qualité de notre modèle ? Nous avons besoin d’une certaine mesure pour calculer la précision de notre modèle.
Examinons différentes mesures pour évaluer le modèle que nous avons créé ci-dessus.
Évaluation des performances du modèle
Nous utiliserons la racine de l’erreur quadratique moyenne (REQM) ou racine de l’écart quadratique moyen (en anglais, Root Mean Square Error = RMSE) et le coefficient de détermination (score R²) pour évaluer notre modèle.
RMSE est la racine carrée de la moyenne de la somme des carrés des valeurs résiduelles.
RMSE est défini par :
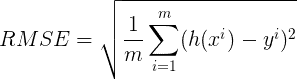
# MSE pour Mean Square Error (erreur quadratique moyenne) mse = np.sum((y_pred - y_actual)**2) # RMSE pour Root Mean Square Error (racine carrée de l'erreur quadratique moyenne) # m est le nombre d'échantillons d'apprentissage rmse = np.sqrt(mse/m)
Le score RMSE est de 2.764182038967211.
LE score R² ou le coefficient de détermination explique dans quelle mesure la variance totale de la variable dépendante peut être réduite en utilisant la régression des moindres carrés.
R² est déterminé par :
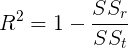
SSₜ est la somme totale des erreurs si l’on prend la moyenne des valeurs observées comme valeur prédite :
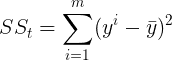
SSᵣ est la somme du carré des résidus :
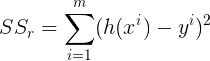
# ssr = sum of square of residuals (somme des carrés des résidus) ssr = np.sum((y_pred - y_actual)**2) # sst = total sum of squares (somme totale des carrés) sst = np.sum((y_actual - np.mean(y_actual))**2) # Score R2 r2_score = 1 - (ssr/sst)
SSₜ - 69.47588572871659 SSᵣ - 7.64070234454893 Score R² - 0.8900236785122296
Si nous utilisons la moyenne des valeurs observées comme valeur prédite, la variance est de 69,47588572871659 et si nous utilisons la régression, la variance totale est de 7,64070234454893. Nous avons réduit l’erreur de prévision d’environ 89 % en utilisant la régression.
Essayons maintenant d’implémenter la régression linéaire à l’aide de la bibliothèque scikit-learn, très populaire en Machine Learning.
Implémentation de la régression linéaire avec scikit-learn
sckit-learn est une bibliothèque très puissante pour la Data Science. Le code complet est donné ci-dessous :
# Importations
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, r2_score
# Générer des données aléatoires
np.random.seed(0)
x = np.random.rand(100, 1)
y = 2 + 3 * x + np.random.rand(100, 1)
# Implémentation avec sckit-learn
# initialisation du modèle
regression_model = LinearRegression()
# Adapter les données (entraînement du modèle)
regression_model.fit(x, y)
# Prédiction
y_predicted = regression_model.predict(x)
# Évaluation du modèle
rmse = mean_squared_error(y, y_predicted)
r2 = r2_score(y, y_predicted)
# Affichage des valeurs
print("Pente : " ,regression_model.coef_)
print("Ordonnée à l'origine : ", regression_model.intercept_)
print("Racine carrée de l'erreur quadratique moyenne : ", rmse)
print('Sccore R2 : ', r2)
# Tracée des valeurs
# Points de données
plt.scatter(x, y, s=10)
plt.xlabel('x')
plt.ylabel('y')
# Valeurs prédites
plt.plot(x, y_predicted, color='r')
plt.show()
Les paramètres du modèle et les mesures de performance du modèle sont indiqués ci-dessous :
Pente : [[2.93655106]] Ordonnée à l'origine : [2.55808002] Racine carrée de l'erreur quadratique moyenne : 0.07623324582875007 Sccore R2 : 0.9038655568672764
C’est presque similaire à ce que nous avons réalisé lorsque nous avons implémenté la régression linéaire from scratch.
Conclusion
C’est terminé pour cet article sur l’algorithme de la régression linéaire. Nous avons appris les concepts de régression linéaire et de la descente de gradient. Nous avons également implémenté le modèle from scratch à partir de code Python puis à l’aide de la bibliothèque scientifique scikit-learn.
J’espère que tout est clair pour vous, vous trouverez le code complet sur ce notebook Google Colab.
Dans l’article suivant de cette série, nous allons prendre un ensemble de données réel et construire un modèle de régression linéaire dessus.
Vous aimerez sans doute aussi en savoir plus sur les différents algorithmes de Machine Learning.