Dans cet article, nous allons entraîner un simple réseau de neurones convolutifs en utilisant Keras avec Python pour une tâche de classification. Pour cela, nous allons utiliser un très petit (et simple) ensemble d’images composé de 100 images de dessins de cercles, 100 images de carrés et 100 images de triangles que j’ai trouvé ici sur Kaggle. Ces images seront divisées en ensembles d’entraînement et de test et alimenteront le réseau. Nous allons passer la répartition entraînement/test car ce n’est pas le sujet de l’article mais je vous fournis bien entendu l’ensemble du code en cliquant ici.
Nous allons reproduire une partie du travail de François Chollet dans son livre Deep Learning avec Python afin d’apprendre comment notre structure de couches traite les données en termes de visualisation de chaque activation intermédiaire. Ce qui consiste à afficher les cartes de features qui sont produites par les couches de convolution et de Pooling dans le réseau.
Ce que cela signifie, c’est que nous allons visualiser le résultat de chaque couche d’activation.
Nous allons aller très vite sur la construction du modèle de réseau de neurones convolutifs car nous ne nous concentrons pas ici sur une explication détaillée des réseaux CNNs avec Keras. Pour une explication complète, vous pouvez consulter ma formation complète de Deep Learning avec Tensorflow 2 et Keras.
Construction d’un réseau de neurones convolutifs avec Keras
Commençons par importer toutes les bibliothèques nécessaires :
import glob import matplotlib from matplotlib import pyplot as plt import matplotlib.image as mpimg import numpy as np import imageio as im from keras import models from keras.models import Sequential from keras.layers import Conv2D from keras.layers import MaxPooling2D from keras.layers import Flatten from keras.layers import Dense from keras.layers import Dropout from keras.preprocessing import image from keras.preprocessing.image import ImageDataGenerator from keras.callbacks import ModelCheckpoint
Images d’entraînement
Voici nos images d’entraînement :
Cercles
images = []
for img_path in glob.glob('training_set/circles/*.png'):
images.append(mpimg.imread(img_path))
plt.figure(figsize=(20,10))
columns = 5
for i, img in enumerate(images):
plt.subplot(len(images) / columns + 1, columns, i + 1)
plt.imshow(img)
Carrés
(le code est à peu près le même que celui ci-dessus, voir le code complet ici)
Triangles
Les formes/dimensions des images sont de 28 pixels par 28 pixels à l’échelle RGB (bien qu’on puisse dire qu’elles sont uniquement en noir et blanc).
Initialisation du Modèle
Procédons maintenant à la construction de notre réseau de neurones convolutif. Comme d’habitude, on initialise le modèle avec Sequential() :
# Initialisation du modèle model = Sequential()
Construction du modèle de réseau de neurones convolutif
Nous spécifions nos couches de convolution et ajoutons MaxPooling pour réduire l’échantillonnage et Dropout pour éviter l’overfitting. Nous utilisons Flatten et terminons avec une couche Dense de 3 neurones, une pour chaque classe (cercle [0], carré [1], triangle [1]). Nous spécifions softmax en tant que fonction d’activation de notre dernière couche (ce qui est suggéré pour la classification multi-classes).
# Convolution model.add(Conv2D(32, (3, 3), padding='same', input_shape = (28, 28, 3), activation = 'relu')) model.add(Conv2D(32, (3, 3), activation='relu')) model.add(MaxPooling2D(pool_size=(2, 2))) model.add(Dropout(0.5)) # Ajout d'une deuxième couche convolutive model.add(Conv2D(64, (3, 3), padding='same', activation = 'relu')) model.add(Conv2D(64, (3, 3), activation='relu')) model.add(MaxPooling2D(pool_size=(2, 2))) model.add(Dropout(0.5)) # Ajout d'une troisième couche convolutive model.add(Conv2D(64, (3, 3), padding='same', activation = 'relu')) model.add(Conv2D(64, (3, 3), activation='relu')) model.add(MaxPooling2D(pool_size=(2, 2))) model.add(Dropout(0.5)) # antes era 0.25 # Flatten model.add(Flatten()) # Connexion complète model.add(Dense(units = 512, activation = 'relu')) model.add(Dropout(0.5)) model.add(Dense(units = 3, activation = 'softmax'))
Pour ce type d’images, il se peut que je construise une structure trop complexe, et cela sera évident lorsque nous regarderons les cartes de features. Cependant, pour les besoins de cet article, cela m’aide à montrer exactement ce que chaque couche fera. Mais, notez que je suis presque certain que nous pouvons obtenir des résultats identiques ou meilleurs avec moins de couches (et donc moins de complexité).
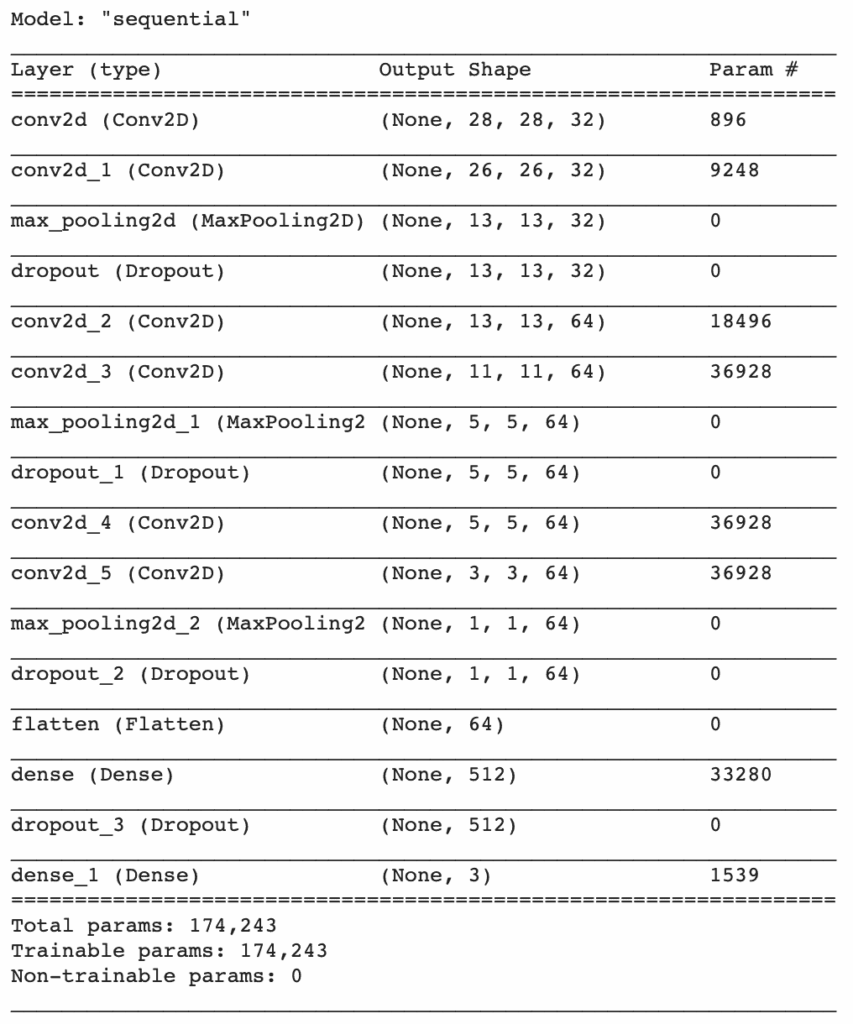
Jetons un coup d’œil au résumé de notre modèle :
model.summary()
Compilation du Modèle
Nous compilons le modèle en utilisant rmsprop comme optimiseur, categorical_crossentropy comme fonction de perte et nous spécifions accuracy comme la métrique que nous voulons suivre :
# Compilation du modèle
model.compile(optimizer = 'rmsprop',
loss = 'categorical_crossentropy',
metrics = ['accuracy'])Utilisation de ImageDataGenerator pour lire des images à partir de répertoires
À ce stade, nous devons convertir nos images en une forme que le modèle acceptera. Pour cela, nous utilisons ImageDataGenerator. Nous l’initialisons et alimentons nos images avec .flow_from_directory. Il y a deux dossiers principaux dans le répertoire de travail, nommés training_set et test_set. Chacun d’eux a 3 sous-dossiers appelés circles, squares et triangles. J’ai envoyé 70 images de chaque forme dans le training_set et 30 dans le test_set.
train_datagen = ImageDataGenerator(rescale = 1./255)
test_datagen = ImageDataGenerator(rescale = 1./255)
batch_size = 16
training_set = train_datagen.flow_from_directory('training_set',
target_size = (28, 28),
batch_size = batch_size,
class_mode = 'categorical')
test_set = test_datagen.flow_from_directory('test_set',
target_size = (28, 28),
batch_size = batch_size,
class_mode = 'categorical')Found 210 images belonging to 3 classes. Found 90 images belonging to 3 classes.
Utilisation du callback pour stocker les poids du meilleur modèle.
Le modèle s’entraînera pendant 30 epochs mais nous utiliserons ModelCheckpoint pour stocker les poids de l’epoch la plus performante parmi ces 30 epochs. Nous allons spécifier val_accuracy comme la métrique à utiliser pour définir le meilleur modèle. Cela signifie que nous conserverons les poids de l’epoch qui obtient le meilleur résultat pour l’exactitude (accuracy) sur l’ensemble de test.
checkpointer = ModelCheckpoint(filepath="best_weights.hdf5",
monitor = 'val_accuracy',
verbose=1,
save_best_only=True)Entraînement du modèle
Maintenant il est temps d’entraîner le modèle, ici nous incluons le callback à notre checkpointer.
history = model.fit(training_set,
batch_size = 100,
epochs = 30,
callbacks=[checkpointer],
validation_data = test_set,
validation_batch_size = 50)Le modèle s’entraîne pendant 30 epochs et atteint sa meilleure performance à l’epoch 27. Nous obtenons le message suivant :
Epoch 00027: val_accuracy improved from 0.86667 to 0.87778, saving model to best_weights.hdf5
Après cela, le modèle ne s’améliore pas pour les epochs suivantes, donc les poids de l’epoch 27 sont ceux qui sont stockés – Cela signifie que nous avons maintenant un fichier hdf5 qui stocke les poids de cette époque spécifique, où la précision sur l’ensemble de test était de 87,7%.
Chargement de notre classificateur avec les poids du meilleur modèle
Nous nous assurerons que notre classificateur est chargé avec les meilleurs poids avec cette ligne de code :
model.load_weights('best_weights.hdf5')Sauvegarde du modèle complet
Et enfin, sauvegardons le modèle final pour une utilisation ultérieure :
model.save('shapes_cnn.h5')Affichage des courbes de loss et de accuracy pendant l’entraînement
Voyons maintenant comment notre modèle s’est comporté pendant les 30 epochs :
acc = history.history['accuracy']
val_acc = history.history['val_accuracy']
loss = history.history['loss']
val_loss = history.history['val_loss']
epochs = range(1, len(acc) + 1)
plt.plot(epochs, acc, 'bo', label="Accuracy d'entraînement")
plt.plot(epochs, val_acc, 'b', label='Accuracy de validation')
plt.title("Accuracy d'entraînement et de validation")
plt.legend()
plt.figure()
plt.plot(epochs, loss, 'bo', label="Perte d'entraînement")
plt.plot(epochs, val_loss, 'b', label='Perte de validation')
plt.title("Perte d'entraînement et de validation")
plt.legend()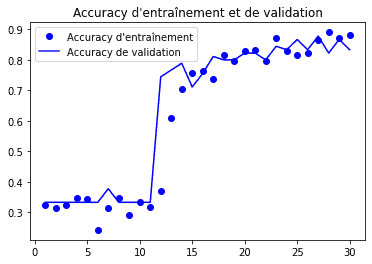
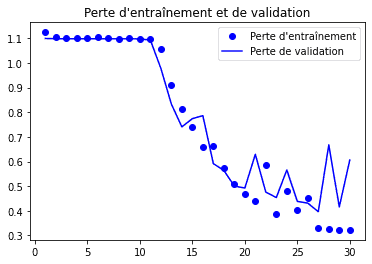
Nous pouvons voir qu’après l’epoch 27, le modèle semble commencer son phénomène d’overfitting. Néanmoins, nous avons gardé les résultats de l’epoch qui avait la meilleure performance.
Classes
Précisons maintenant le numéro de classe attribué à chacun de nos ensembles de chiffres, puisque c’est ainsi que le modèle produira ses prédictions :
- circles : 0
- squares : 1
- triangles : 2
Prédiction de la classe de nouvelles images inconnues
Une fois notre modèle entraîné et stocké, nous pouvons charger une simple image (inconnue de notre ensemble de test) et voir comment elle est classifiée :
img_path = 'test_set/triangles/drawing(1).png' img = image.load_img(img_path, target_size=(28, 28)) img_tensor = image.img_to_array(img) img_tensor = np.expand_dims(img_tensor, axis=0) img_tensor /= 255. plt.imshow(img_tensor[0]) print(img_tensor.shape)
Prédiction d’images
# Prédiction d'images
x = image.img_to_array(img)
x = np.expand_dims(x, axis=0)
images = np.vstack([x])
classes = np.argmax(model.predict(images, batch_size=10), axis=-1)
print("La classe prédite est :",classes)La classe prédite est : [2]
La prédiction est la classe [2] qui est un triangle.
Jusqu’ici tout va bien. Nous passons maintenant à la partie la plus importante de cet article.
Visualisation des activations intermédiaires
Je cite François Chollet dans son livre Deep Learning with Python (et je le citerai beaucoup dans cette section) :
Les activations intermédiaires sont « utiles pour comprendre comment les couches successives du convnet transforment leur entrée, et pour avoir une première idée de la signification des filtres individuels du convnet ».
« Les représentations apprises par les convnets se prêtent bien à la visualisation, en grande partie parce qu’il s’agit de représentations de concepts visuels. La visualisation des activations intermédiaires consiste à afficher les cartes de caractéristiques qui sont produites par les différentes couches de convolution et de mise en commun d’un réseau, compte tenu d’une certaine entrée (la sortie d’une couche est souvent appelée son activation, la sortie de la fonction d’activation). Cela donne un aperçu de la manière dont une entrée est décomposée en différents filtres appris par le réseau. Chaque canal code des caractéristiques relativement indépendantes, de sorte que la bonne façon de visualiser ces cartes de caractéristiques est de tracer indépendamment le contenu de chaque canal sous la forme d’une image 2D. »
Ensuite, nous allons recevoir une image d’entrée – la photo d’un triangle, qui ne fait pas partie des images sur lesquelles le réseau a été entraîné.
« Afin d’extraire les cartes des features que nous voulons examiner, nous allons créer un modèle Keras qui prend des lots (batches) d’images en entrée et produit les activations de toutes les couches de Convolution et de Pooling. Pour ce faire, nous allons utiliser la classe Model de Keras. Un modèle est instancié en utilisant deux arguments : un tenseur d’entrée (ou une liste de tenseurs d’entrée) et un tenseur de sortie (ou une liste de tenseurs de sortie). La classe résultante est un modèle Keras, tout comme les modèles séquentiels, qui met en correspondance les entrées spécifiées avec les sorties spécifiées. Ce qui distingue la classe Model, c’est qu’elle autorise les modèles à sorties multiples, contrairement à Sequential. »
Instanciation d’un modèle à partir d’un tenseur d’entrée et d’une liste de tenseurs de sortie
# Extrait les sorties (outputs) des 12 couches supérieures layer_outputs = [layer.output for layer in model.layers[:12]] # Crée un modèle qui retournera ces sorties (outputs), étant donné l'entrée (input) du modèle. activation_model = models.Model(inputs=model.input, outputs=layer_outputs)
Lorsqu’il reçoit une image en entrée, ce modèle renvoie les valeurs des activations des couches du modèle d’origine.
Exécution du modèle en mode prédiction
# Retourne une liste de cinq tableaux NumPy : un tableau par activation de couche activations = activation_model.predict(img_tensor)
Par exemple, voici l’activation de la première couche de convolution pour l’entrée image :
first_layer_activation = activations[0] print(first_layer_activation.shape)
(1, 28, 28, 32)
Il s’agit d’une carte de features 28 × 28 avec 32 canaux. Essayons de tracer le quatrième canal de l’activation de la première couche du modèle d’origine :
plt.matshow(first_layer_activation[0, :, :, 4], cmap='viridis')
Avant même d’essayer d’interpréter cette activation, traçons plutôt toutes les activations de cette même image à travers chaque couche.
Visualisation de chaque canal dans chaque activation intermédiaire
Le code complet de cette section pour obtenir le graphique ci-dessous peut être trouvé ici.
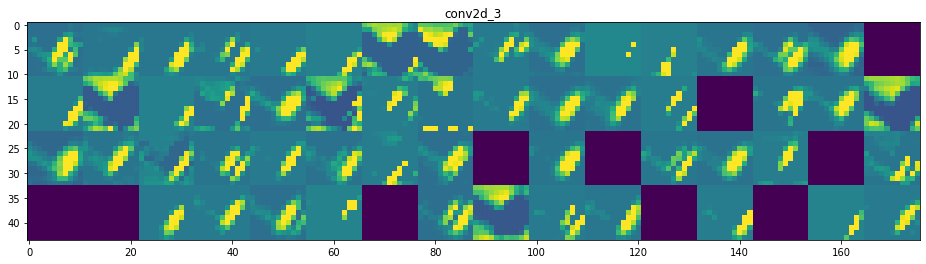
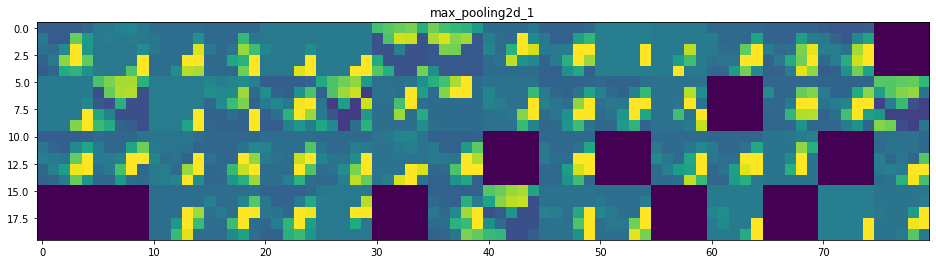
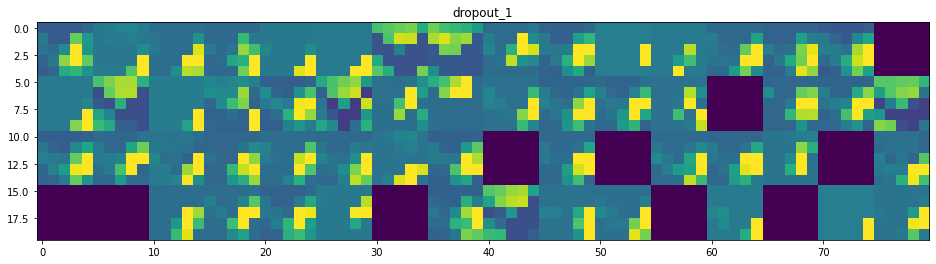
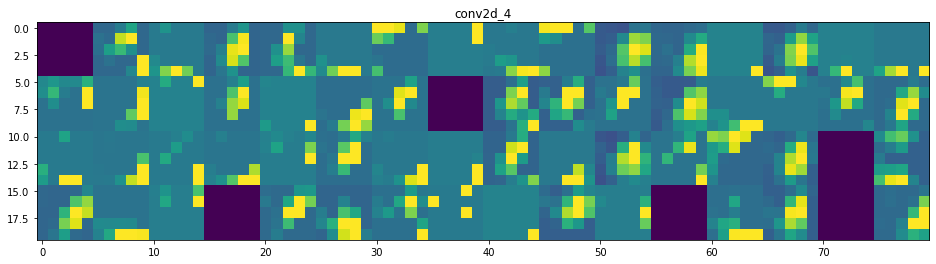
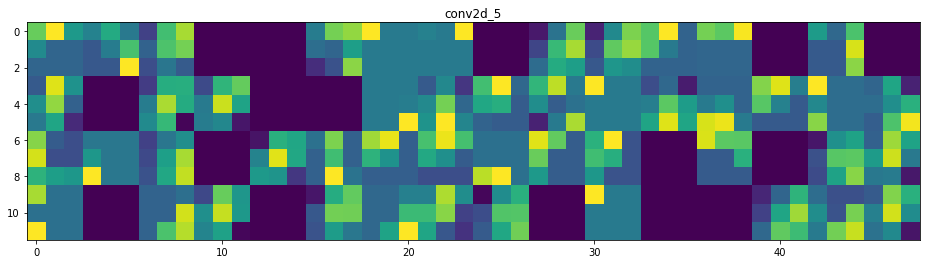
Et voilà ! Essayons d’interpréter ce qui se passe :
- On peut dire que la première couche retient la forme complète du triangle, bien que plusieurs filtres ne soient pas activés et soient laissés en blanc. À ce stade, les activations retiennent presque toutes les informations présentes dans l’image initiale.
- Plus nous descendons dans les couches, plus les activations deviennent abstraites et moins interprétables visuellement. Elles commencent à encoder des concepts de plus haut niveau tels que les bordures simples, les coins et les angles. Les présentations supérieures véhiculent de moins en moins d’informations sur le contenu visuel de l’image, et de plus en plus d’informations liées à la classe de l’image.
- Comme nous l’avons mentionné plus haut, la structure du modèle est excessivement complexe, au point que nous pouvons voir nos dernières couches ne pas s’activer du tout, il n’y a plus rien à apprendre à ce stade.
Nous avons donc visualisé comment un réseau de neurones convolutif trouve des modèles dans certaines figures de base et comment il transporte l’information d’une couche à l’autre.
J’espère que cet article vous a plu, veuillez trouver le code complet dans ce notebook. Et si le Deep Learning vous intéresse, je ne peux que vous recommander mon cours complet sur le sujet : Deep Learning avec Tensorflow 2 et Keras.
