La popularité des crypto monnaies a explosé en 2017 en raison de plusieurs mois consécutifs de croissance exponentielle de leur capitalisation boursière. Les prix ont atteint un sommet de plus de 800 milliards de dollars en janvier 2018. D’où un projet de prédiction du prix des crypto monnaies avec du Deep Learning.
Bien que le Machine Learning ait réussi à prédire les cours boursiers grâce à une multitude de modèles de séries temporelles, son application à la prédiction des prix des prix de crypto monnaies a été assez restrictive. La raison en est évidente, car les prix des crypto monnaies dépendent de nombreux facteurs tels que le progrès technologique, la concurrence interne, la pression exercée sur les marchés pour qu’ils livrent, les problèmes économiques, les questions de sécurité, le facteur politique, etc. Leur grande volatilité conduit à un grand potentiel de profit élevé si des stratégies d’invention intelligentes sont prises. Malheureusement, en raison de leur absence d’indices, les crypto monnaies sont relativement imprévisibles par rapport aux prévisions financières traditionnelles comme les prédictions boursières.
Dans cet article, je vais passer par un processus en quatre étapes pour réaliser la prédiction du prix des crypto monnaies avec du Deep Learning :
- Obtenir des données en temps réel sur les crypto monnaies.
- Préparer les données pour l’entrainement et le test.
- Prévoir le prix des crypto monnaies en utilisant le réseau de neurones LSTM.
- Visualiser les résultats de la prédiction.
Défi à relever
Prédiction du prix des crypto monnaies en utilisant toutes les caractéristiques (features) de Trading comme le prix, le volume, l’ouverture, les valeurs hautes et basses présentes dans l’ensemble de données.
Données
L’ensemble de données peut être téléchargé à partir du site web CryptoCompare en cliquant ici.
L’ensemble de données contient un total de 5 features (caractéristiques/variables). Les détails de ces features sont les suivants :
- Close Price – Il s’agit du prix de clôture du marché des devises pour ce jour particulier.
- High Price – Il s’agit du prix le plus élevé de la devise pour la journée.
- Low Price – Il s’agit du prix le plus bas de la devise pour ce jour.
- Open Price – C’est le prix d’ouverture du marché pour la devise pour ce jour.
- Volume – Le volume de devises échangées ce jour-là.
Code pour la prédiction du prix des crypto monnaies
Maintenant que l’objectif est clair, commençons par le code. Vous pouvez trouver le code du projet complet ici.
Importation des bibliothèques
J’ai commencé par charger toutes les bibliothèques et dépendances nécessaires.
%tensorflow_version 2.x import json import requests from keras.models import Sequential from keras.layers import Activation, Dense, Dropout, LSTM import matplotlib.pyplot as plt import numpy as np import pandas as pd import seaborn as sns from sklearn.metrics import mean_absolute_error
Extraction des données
J’ai utilisé le taux de change européen et j’ai stocké les données en temps réel dans un DataFrame pandas. J’ai utilisé la méthode to_datetime() pour convertir la chaîne (string) Datetime en objet Python Datetime. Ceci est nécessaire car les objets Datetime dans le fichier sont lus comme un objet string. Il est très facile d’effectuer des opérations telles que la différence de temps sur une chaîne plutôt que sur un objet Datetime.
endpoint = 'https://min-api.cryptocompare.com/data/histoday'
res = requests.get(endpoint + '?fsym=BTC&tsym=EUR&limit=500')
hist = pd.DataFrame(json.loads(res.content)['Data'])
hist = hist.set_index('time')
hist.index = pd.to_datetime(hist.index, unit='s')
# colonne cible
target_col = 'close'
# maj API, suppression des 2 colonnes string
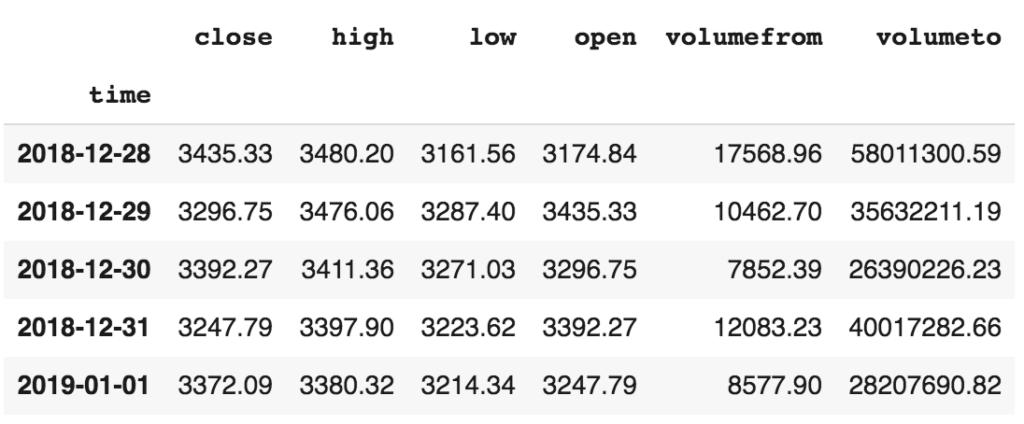
hist = hist.drop(['conversionType','conversionSymbol'], axis=1)Voyons à quoi ressemble l’ensemble de données avec toutes les features de trading comme le prix, le volume, le prix à l’ouverture (open), le prix le plus élevé (high) et le prix le plus bas (low).
hist.head(5)
Séparation des données en 2 ensembles : training et test
Ensuite, j’ai divisé les données en deux ensembles – un ensemble d’entrainement et un ensemble de test avec respectivement 80 % et 20 % de données. La décision prise ici l’est uniquement dans le cadre de ce tutoriel. Dans les projets réels, vous devez toujours diviser vos données en trois parties : entrainement, validation et test (par exemple 60%, 20%, 20%).
def train_test_split(df, test_size=0.2):
split_row = len(df) - int(test_size * len(df))
train_data = df.iloc[:split_row]
test_data = df.iloc[split_row:]
return train_data, test_data
train, test = train_test_split(hist, test_size=0.2)Visualisation des données
Traçons maintenant les prix des crypto monnaies en euros en fonction du temps en utilisant le code ci-dessous :
def line_plot(line1, line2, label1=None, label2=None, title='', lw=2):
fig, ax = plt.subplots(1, figsize=(13, 7))
ax.plot(line1, label=label1, linewidth=lw)
ax.plot(line2, label=label2, linewidth=lw)
ax.set_ylabel('prix [EUR]', fontsize=14)
ax.set_title(title, fontsize=16)
ax.legend(loc='best', fontsize=16)
line_plot(train[target_col], test[target_col], 'training', 'test', title='')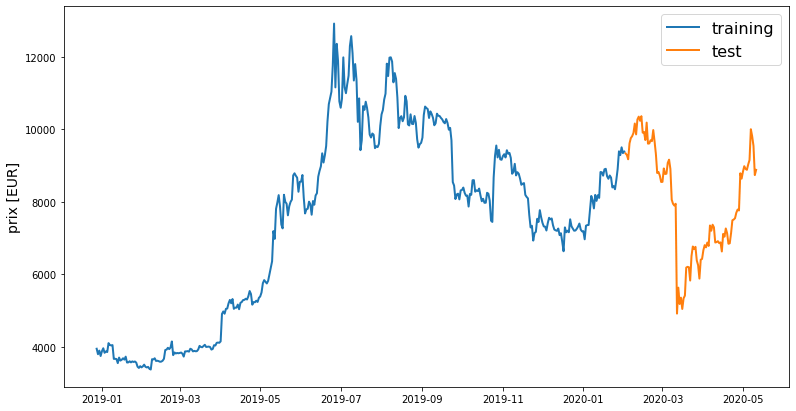
On observe une nette augmentation des prix entre janvier et juillet 2019. Les prix diminuent de juillet 2019 à janvier 2020 avec des fluctuations. À partir de janvier 2020, les prix remontent puis s’effondrent en mars et remontent remontent. Il est intéressant de noter que les prix sont les plus bas en hiver et qu’ils augmentent en été. Bien que cela ne puisse pas être généralisé car l’ensemble de données considéré n’est qu’un petit échantillon qui porte sur une année. De plus, avec la crypto monnaie, il est difficile de généraliser quoi que ce soit.
Préparation des données pour le Deep Learning
Ensuite, j’ai fait quelques fonctions pour normaliser les valeurs. La normalisation est une technique souvent appliquée dans le cadre de la préparation des données pour le Machine Learning. Le but de la normalisation est de changer les valeurs des colonnes numériques de l’ensemble de données à une échelle commune, sans déformer les différences dans les plages de valeurs.
def normalise_zero_base(df):
return df / df.iloc[0] - 1
def normalise_min_max(df):
return (df - df.min()) / (data.max() - df.min())Ensuite, j’ai fait une fonction pour extraire les données des fenêtres qui sont de taille 5 chacune comme indiqué dans le code ci-dessous :
def extract_window_data(df, window_len=5, zero_base=True):
window_data = []
for idx in range(len(df) - window_len):
tmp = df[idx: (idx + window_len)].copy()
if zero_base:
tmp = normalise_zero_base(tmp)
window_data.append(tmp.values)
return np.array(window_data)J’ai continué à faire une fonction pour préparer les données dans un format qui sera ensuite introduit dans le réseau de neurones. J’ai utilisé le même concept de division des données en deux ensembles – un ensemble d’entraînement et un ensemble de test avec respectivement 80 % et 20 % de données, comme le montre le code ci-dessous :
def prepare_data(df, target_col, window_len=10, zero_base=True, test_size=0.2):
train_data, test_data = train_test_split(df, test_size=test_size)
X_train = extract_window_data(train_data, window_len, zero_base)
X_test = extract_window_data(test_data, window_len, zero_base)
y_train = train_data[target_col][window_len:].values
y_test = test_data[target_col][window_len:].values
if zero_base:
y_train = y_train / train_data[target_col][:-window_len].values - 1
y_test = y_test / test_data[target_col][:-window_len].values - 1
return train_data, test_data, X_train, X_test, y_train, y_testRéseau de neurones LSTM : prédiction du prix des crypto monnaies
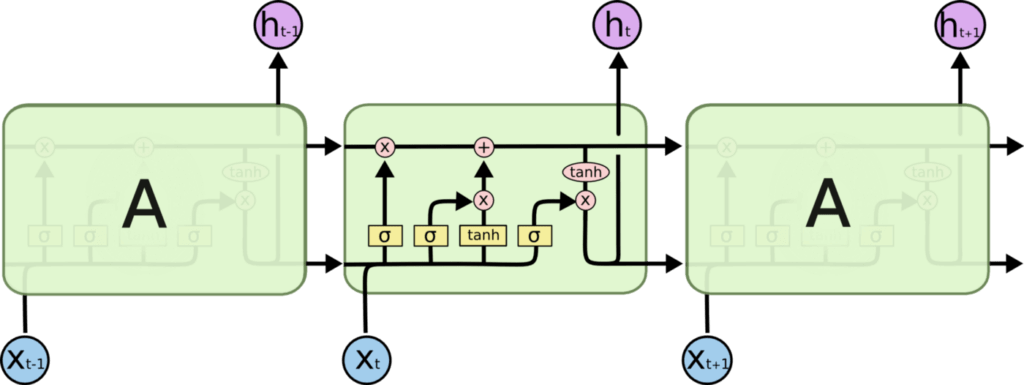
Il fonctionne en utilisant des portes spéciales pour permettre à chaque couche LSTM de prendre des informations à la fois des couches précédentes et de la couche actuelle. Les données passent par plusieurs portes (comme forget gate, input gate, etc.) et diverses fonctions d’activation (comme la fonction tanh, la fonction relu) et sont transmises aux cellules LSTM. Le principal avantage de cette méthode est qu’elle permet à chaque cellule LSTM de se souvenir des motifs pendant un certain temps. Il faut noter que les cellules LSTM peuvent se souvenir d’informations importantes et en même temps oublier des informations non pertinentes.
Les architectures LSTM sont présentées ci-dessous :
Construction du modèle
Maintenant, construisons le modèle. Le modèle séquentiel est utilisé pour empiler toutes les couches (entrée, cachée et sortie). Le réseau de neurones comprend une couche LSTM suivie d’une couche 20 % d’abandon et d’une couche dense avec fonction d’activation linéaire. J’ai respecté le modèle en utilisant Adam comme optimiseur et l’erreur quadratique moyenne comme fonction de perte.
def build_lstm_model(input_data, output_size, neurons=100, activ_func='linear', dropout=0.2, loss='mse', optimizer='adam'):
model = Sequential()
model.add(LSTM(neurons, input_shape=(input_data.shape[1], input_data.shape[2])))
model.add(Dropout(dropout))
model.add(Dense(units=output_size))
model.add(Activation(activ_func))
model.compile(loss=loss, optimizer=optimizer)
return modelParamètres du modèle
Ensuite, j’ai défini certains des paramètres à utiliser plus tard. Ces paramètres sont les suivants : nombre aléatoire de seed, longueur de la fenêtre, taille de l’ensemble de test, nombre de neurones dans la couche LSTM, epochs, taille du lot (batch), perte, dropout et optimiseur.
np.random.seed(42) window_len = 5 test_size = 0.2 zero_base = True lstm_neurons = 100 epochs = 20 batch_size = 32 loss = 'mse' dropout = 0.2 optimizer = 'adam'
Entrainement du modèle
Maintenant, entrainons le modèle en utilisant les entrées x_train et les étiquettes y_train.
train, test, X_train, X_test, y_train, y_test = prepare_data(
hist, target_col, window_len=window_len, zero_base=zero_base, test_size=test_size)
model = build_lstm_model(
X_train, output_size=1, neurons=lstm_neurons, dropout=dropout, loss=loss,
optimizer=optimizer)
history = model.fit(
X_train, y_train, epochs=epochs, batch_size=batch_size, verbose=1, shuffle=True)Jetons un coup d’oeil à l’entrainement des modèles pour 20 cycles ou epochs.
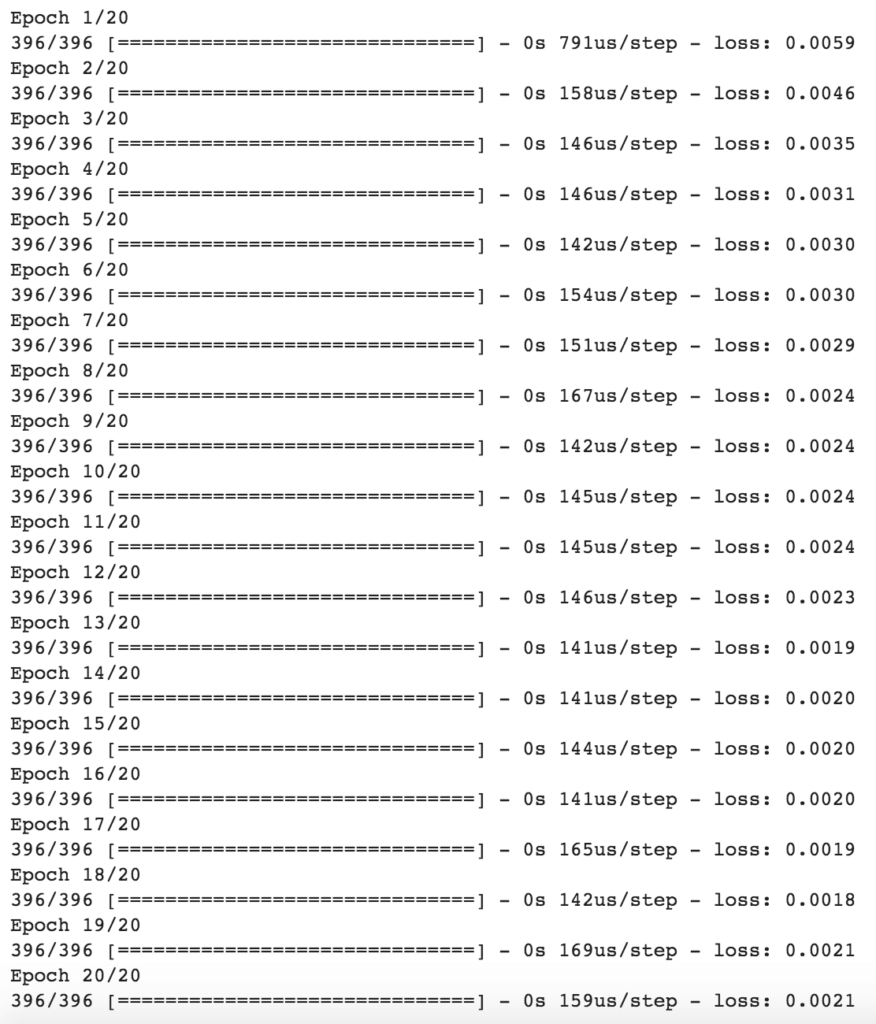
J’ai utilisé l’erreur moyenne absolue (Mean Absolute Error – MAE) comme mesure d’évaluation. La raison pour laquelle j’ai choisi la MAE plutôt que l’erreur quadratique moyenne (Means Square Error – MSE) est que la MAE est plus facile à interpréter. La RMSE (Root Mean Square Error) ne décrit pas seulement l’erreur moyenne et est donc beaucoup plus difficile à comprendre. Comme nous voulons que le modèle soit facilement expliqué même à un public non technique, la MAE semble être un meilleur choix.
Erreur Moyenne Absolue (MAE)
Cela mesure l’ampleur moyenne des erreurs dans un ensemble de prédictions, sans tenir compte de leur direction. C’est la moyenne sur l’échantillon test des différences absolues entre les observations réelles et prédites, où toutes les différences individuelles ont le même poids.
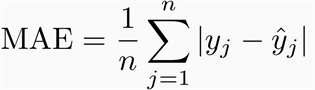
targets = test[target_col][window_len:] preds = model.predict(X_test).squeeze() mean_absolute_error(preds, y_test)
0.0402736625666246
La valeur du MAE obtenue semble bonne.
Enfin, nous allons tracer les prix réels et leurs prédictions en utilisant le code ci-dessous :
preds = test[target_col].values[:-window_len] * (preds + 1) preds = pd.Series(index=targets.index, data=preds) line_plot(targets, preds, 'actual', 'prediction', lw=3)
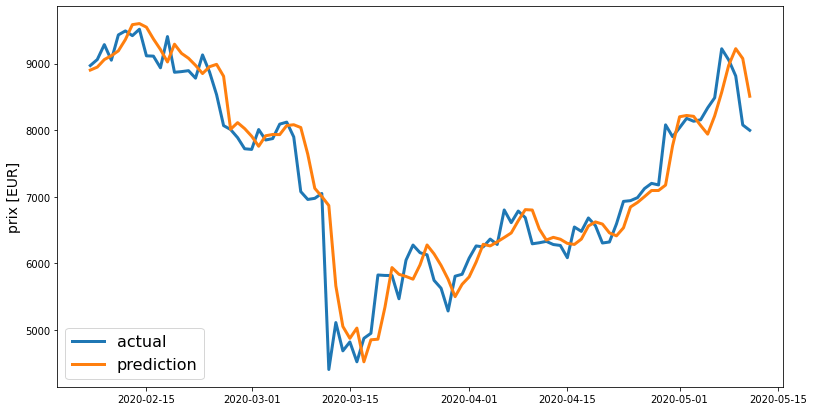
Conclusion
Dans cet article, j’ai démontré comment prédire les prix des crypto monnaies en temps réel en utilisant le réseau de neurones LSTM. J’ai suivi un processus en quatre étapes consistant à obtenir des données sur les crypto monnaies en temps réel, à préparer les données pour l’entrainement et les tests, à prédire les prix à l’aide du réseau de neurones LSTM et à visualiser les résultats de la prédiction. N’hésitez pas à jouer avec les hyper-paramètres ou à essayer différentes architectures de réseau de neurones pour obtenir de meilleurs résultats.
