Un aperçu pratique avec des exemples et du code Python.
Les distributions de probabilité sont des fonctions mathématiques décrivant les probabilités que certaines choses se produisent. Finalement, de nombreux processus qui se déroulent dans le monde qui nous entoure peuvent être décrits par quelques distributions de probabilité qui ont déjà été bien étudiées et analysées. La maîtrise de ces quelques distributions permet de modéliser statistiquement toute une série de phénomènes. Jetons un coup d’œil à 6 distributions de probabilités bien utiles !
Dans cet article, on passe en revue 6 distributions de probabilités, pour en savoir plus, je vous recommande de consulter mon cours Probabilité et Statistiques pour la Data Science et Business (si ce n’est pas déjà fait 🙂 ).
Distribution Binomiale
La distribution binomiale est sans doute la distribution de probabilité à la fois la plus intuitive et la plus puissante. Elle peut être utilisée pour modéliser des données binaires, c’est-à-dire des données qui ne peuvent prendre que deux valeurs différentes, par exemple : « oui » ou « non ». Cela rend la distribution binomiale appropriée pour les décisions de modélisation ou d’autres processus, tels que :
- Le client a-t-il acheté le produit, ou non ?
- Est-ce que le médicament a aidé le patient à se rétablir, ou non ?
- L’ annonce en ligne a-t-elle été cliquée ou non ?
Les deux éléments clés du modèle binomial sont : un ensemble d’épreuves (expériences binaires) et la probabilité de succès (le succès est le résultat « oui » : une annonce cliquée ou un patient guéri). Par exemple, les épreuves peuvent consister à lancer 10 fois une pièce de monnaie — chacun d’eux est une expérience binaire avec deux résultats possibles : Pile ou Face. La probabilité de succès, définie comme retourner la pièce sur Face, est de 50%, en supposant que la pièce est équilibrée.
La distribution binomiale peut répondre à la question : quelle est la probabilité d’observer un nombre variable d’évènements « la pièce s’est retournée sur le côté Face » en 10 lancers (d’une pièce équilibrée) ?
from scipy.stats import binom
import matplotlib.pyplot as plt
num_trials = 10
heads_probability = .5
probs = [binom.pmf(i, num_trials, heads_probability) for i in range(11)]
plt.stem(list(range(11)), probs, use_line_collection=True)
plt.title("Probabilité d'obtenir X retournement(s) sur Face lors de 10 lancers à pile ou face")
plt.xlabel('Nombre de retournement sur Face')
plt.ylabel('Probabilité');
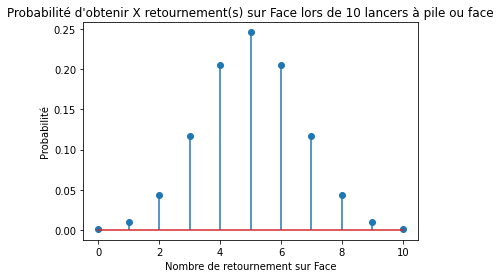
La fonction de masse de la loi de probabilité binomiale tracée ci-dessus est la réponse ! Vous pouvez voir qu’il est le plus susceptible d’observer 5 côtés Face avec 10 lancers, et la probabilité d’un tel résultat est d’environ 25%.
Un exemple d’utilisation pratique de la distribution binomiale est de modéliser les clics par rapport aux non-clics sur une bannière publicitaire, où la probabilité de succès est le taux de clics. La distribution binomiale peut servir de détecteur d’anomalies. Supposons que vous avez affiché votre annonce auprès de 750 utilisateurs et 34 ont cliqué dessus. Cela donne un taux de clics de 4,5 %. Si vous savez que le taux moyen de clics pour toutes vos annonces précédentes était de 6 %, vous pouvez vous demander : quelle est la probabilité de ne pas observer plus de 4,5 % cette fois ? Pour répondre à cela, vous pouvez modéliser vos clics avec une distribution binomiale avec la probabilité de succès de 6%, ce qui ressemble à ceci :
num_trials = 750
heads_probability = .06
probs = [binom.pmf(i, num_trials, heads_probability) for i in range(751)]
plt.stem(list(range(751)), probs, use_line_collection=True)
plt.xlim([0, 150])
plt.title("Probabilité d'obtenir X clics avec 750 impressions")
plt.xlabel('Nombre de clics')
plt.ylabel('Probabilité');
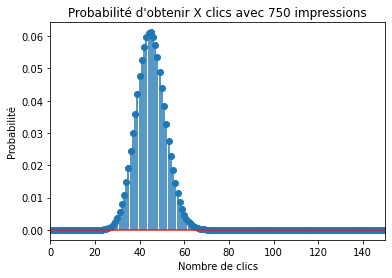
Alors, quelle est la probabilité de ne pas observer plus de 34 clics en 750 impressions ? La réponse est la somme de toutes les barres de 0 à 34, ou : binom.cdf(34, 750, 0.06) qui est de 4,88%, c’est tout à fait improbable. Soit la nouvelle annonce est vraiment mauvaise, soit quelque chose de louche se passe ici…
Êtes-vous sûr que votre fournisseur d’annonces l’a réellement affiché à 750 utilisateurs ?
La loi binomiale décrit les données oui / non. Elle peut servir de détecteur d’anomalies ou d’outil pour les tests Bayésiens (Tests A/B).
Une autre application courante de la loi binomiale est pour les tests A/B bayésiens. Imaginez que vous ayez mené deux campagnes marketing et que vous voulez les comparer. Une simple comparaison de deux taux de clics peut être trompeuse, car il y a une composante aléatoire dans les deux, et l’un peut sembler plus élevé que l’autre en raison du hasard seul. Il y a deux façons d’établir quelle campagne était la meilleure : vous pouvez soit recourir à des tests d’hypothèse classiques (ou tests statistiques), soit estimer explicitement la probabilité que la campagne A était meilleure que la campagne B avec l’approche bayésienne. Ce dernier suppose que les clics suivent la loi binomiale et que le calcul des probabilités postérieures bayésiennes implique la formule de densité binomiale.
Distribution de Poisson
Une autre distribution très utile est la distribution de Poisson. Tout comme la distribution binomiale, c’est aussi une distribution discrète, ce qui signifie qu’elle a un ensemble limité de résultats possibles. Pour la distribution binomiale, il n’y en avait que deux : oui ou non (succès ou échec). Pour la distribution de Poisson, il peut y en avoir plus, mais ils ne peuvent être que des entiers naturels : 0, 1, 2, et ainsi de suite.
La distribution de Poisson peut être utilisée pour décrire les événements qui se produisent à un certain rythme dans le temps ou l’espace. De tels processus sont omniprésents : les clients font un achat dans votre boutique en ligne toutes les X minutes, et chaque produit sur Y sortant de la chaîne d’assemblage est défectueux.
La loi de Poisson a un paramètre, généralement désigné par une lettre grecque λ (lambda), qui indique le rythme (ou fréquence) à laquelle les événements se produisent. Le cas d’utilisation typique consiste à estimer λ à partir des données, puis à utiliser la distribution résultante pour effectuer des simulations de mise en file d’attente qui aident à allouer des ressources.
Imaginez que vous ayez un modèle de Machine Learning déployé dans le cloud et que vous receviez les requêtes de vos clients en temps réel. Combien de ressources cloud devez-vous payer pour être sûr à 99 % que vous pouvez desservir tout le trafic qui arrive dans le modèle dans une période d’une minute ? Pour répondre à cette question, vous devez d’abord savoir combien de requêtes arrivent, en moyenne, en une minute. Par exemple cela peut être 3,3 requêtes en moyenne en fonction de vos données de trafic. Il s’agit de votre λ, et donc la distribution de Poisson décrivant vos données ressemble à ceci :
rate = 3.3
probs = [poisson.pmf(i, rate) for i in range(15)]
plt.stem(list(range(15)), probs, use_line_collection=True)
plt.title("Probabilité que X requête(s) arrive(nt) dans une période d'une minute")
plt.xlabel('Nombre de requête(s) par minute')
plt.ylabel('Probabilité');
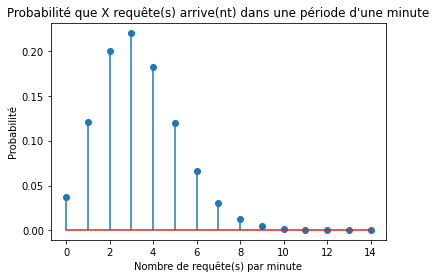
Sur la base de votre distribution de Poisson, vous pouvez calculer la probabilité d’observer 2 événements en une minute : poisson.pmf(2, 3.3), qui donne 20%, ou la probabilité d’obtenir 5 requêtes ou moins : poisson.cdf(5, 3.3) qui est de 88%.
La distribution de Poisson décrit les événements qui se produisent à un certain rythme dans l’espace temporel. Il peut être utilisé pour effectuer des simulations de mise en file d’attente qui aident à allouer des ressources.
Okay cool, mais la question était : combien de demandes par minute devez-vous être en mesure d’effectuer pour que vous puissiez être sûr de traiter tout le trafic à 99% ? Une façon de répondre à cela est de simuler beaucoup (disons, 1 000 000) de périodes d’une minute et de calculer le 99e percentile du nombre de demandes.
simulated_request_per_minute = poisson.rvs(3.3, size=1_000_000) np.percentile(simulated_request_per_minute, 99)
Cela donne 8, ce qui signifie que si vous achetez suffisamment de ressources pour traiter 8 demandes par minute, vous pouvez être sûr à 99% de traiter tout le trafic dans n’importe quelle période d’une minute.
Distribution Exponentielle
Une autre distribution, étroitement liée à la distribution de Poisson, est la distribution exponentielle. Si le nombre d’événements survenus au cours d’une certaine période suit le processus de Poisson, alors le temps entre ces événements est décrit par la distribution exponentielle.
Poursuivant l’exemple précédent, si nous observons 3,3 demandes par minute en moyenne, nous pouvons modéliser le temps entre les demandes en utilisant la distribution exponentielle. Exprions-le en quelques secondes : 3,3 requêtes par minute est 0,055 requêtes par seconde. Une mise en garde est que dans le paquet scipy de Python, la distribution exponentielle est paramétrée avec une échelle, qui est l’inverse d’un taux. De plus, la distribution exponentielle est continue plutôt que discrète, ce qui signifie qu’elle peut prendre infiniment des valeurs. Pour souligner cela, nous la traçons comme une zone grisée plutôt que comme des barres verticales. La distribution en question se présente comme suit :
import numpy as np
import seaborn as sns
scale = 1 / 3.3
exp = np.random.exponential(scale, size = 1_000_000)
sns.kdeplot(exp, shade=True, color='xkcd:lightish blue')
plt.title("Probabilité que X minute(s) s'écoule(nt) entre deux événements")
plt.xlabel('Nombre de minute(s) entre 2 évènements')
plt.ylabel('Densité');
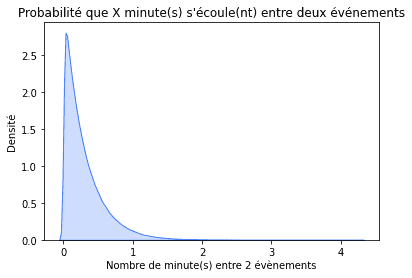
Avec un taux moyen de plus de trois demandes par minute, dans la plupart des cas, il ne s’écoulera pas plus d’une minute entre une demande et une autre. Parfois, cependant, il peut s’écouler jusqu’à cinq minutes sans qu’aucune demande ne soit reçue !
Tout comme la distribution binomiale, la distribution exponentielle peut également servir de détecteur d’anomalies. Une fois que vous n’avez pas vu de demande pendant 5 minutes, vous pouvez commencer à vous demander si vos systèmes sont toujours en vie. Quelle est la probabilité que cinq minutes ou plus s’écoulent sans demande ? C’est la somme de toutes les barres à partir de cinq et à droite jusqu’à l’infini, ce qui équivaut à un moins les barres à gauche de cinq puisque la somme de toutes les barres doit être un. Donc, c’est 1 — expon.cdf(4, 1/3.3), ce qui est 2,5%. Pas très probable, mais cela peut se produire de temps en temps.
La distribution exponentielle peut être utilisée comme détecteur d’anomalies ou comme simple repère pour les modèles prédictifs.
Un autre cas d’utilisation courant de la distribution exponentielle est celui d’un simple benchmark pour les modèles prédictifs. Par exemple, pour prédire quand un produit sera à nouveau acheté, vous pouvez utiliser le boosting de gradient ou construire un réseau neuronal sophistiqué. Pour évaluer leur performance, il est recommandé de les comparer à un simple benchmark. Si vous dites que votre problème prédit la durée jusqu’au prochain achat, alors la distribution exponentielle est une excellente référence. Une fois que vous avez les données d’entraînement (days_till_next_purchase = [1, 4, 2, 2, 3, 6,...,]), il suffit d’adapter la distribution exponentielle à ces données et de prendre sa signification comme prédiction : avg, _ = expon.fit(days_till_next_purchase).
Distribution Normale
La distribution normale, également connue sous le nom de courbe de cloche (ou distribution Gaussienne), est peut-être la plus célèbre, et aussi la plus largement utilisée — bien que souvent implicitement.
Tout d’abord, le théorème Central Limite (TCL), qui est la pierre angulaire de l’inférence statistique, est au centre du concept de la distribution normale. Je vous encourage à en savoir plus à ce sujet ici : Théorème Central Limite sur Wikipédia.
En résumé, le TCL établit que certaines statistiques, telles qu’une somme ou une moyenne, calculées à partir d’échantillons aléatoires de données suivent la distribution normale. Les deux cas d’utilisation pratiques les plus importants pour le TCL sont l’analyse de régression et le test d’hypothèses.
Tout d’abord, parlons de régression. Dans un modèle de régression, la variable dépendante est expliquée par certaines variables prédictives plus un terme d’erreur, que nous supposons être normalement distribués. Cette normalité supposée de l’erreur découle du TCL : nous pouvons considérer l’erreur comme la somme de nombreuses erreurs indépendantes causées par l’omission de prédicteurs importants ou par le hasard. Chacune de ces nombreuses erreurs peut avoir n’importe quelle distribution, mais leur somme sera approximativement normale de par le TCL.
L’ hypothèse de normalité d’erreurs dans les modèles de régression peut être justifiée par le Théorème Central Limite. Il est également utile pour certains tests d’hypothèses.
Deuxièmement, les tests d’hypothèses. Des exemples plus élaborés suivront sous peu lorsque nous parlerons des distributions Chi carré et F. Pour l’instant, prenons ce bref exemple : une entreprise spécialisée dans le reciblage publicitaire se vante que ses annonces ciblées avec précision reçoivent un taux de clics de 20 % en moyenne. Vous exécutez un pilote de 1000 impressions avec eux et observez 160 clics, ce qui signifie un taux de clics de seulement 16%. Le ciblage n’est-il pas aussi bon, ou était-ce juste de la malchance ?
Si vous considérez les 1000 utilisateurs auxquels les annonces ont été affichées comme un sous-ensemble aléatoire provenant de la plus grande population d’utilisateurs, alors le TCL entre en jeu et le taux de clics devrait suivre une distribution normale. En supposant que la société de ciblage dise la vérité, il devrait s’agir d’une distribution normale avec une moyenne de 0,2 et un écart-type de 0,013. La distribution en question se présente comme suit :
mu, sigma = 0.2, 0.013
normal = np.random.normal(loc=mu, scale=sigma, size=1000)
sns.kdeplot(normal, shade=True, color='xkcd:lightish blue')
plt.axvline(x=0.16,color='r', linestyle='--',label='CTR observé de 0.16')
plt.title("Distribution de référence du Taux de Clics (CTR) par rapport au CTR observé")
plt.xlabel('Taux de clics')
plt.ylabel('Densité');
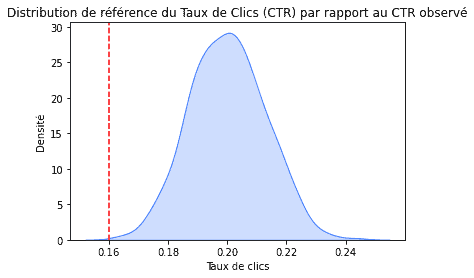
Selon cette distribution, le taux de clics de 16 % que vous avez observé est plutôt improbable, ce qui indique que la prétendue moyenne de 20 % est très probablement fausse.
Distribution Chi-carré
La distribution χ2 ou chi-carré est très pratique dans les tests A/B/C. Imaginez que vous avez mené une expérience dans laquelle vous avez affiché votre site Web de manière aléatoire dans différentes versions de couleurs pour les utilisateurs. Vous êtes curieux de savoir quelle couleur mène au plus grand nombre d’achats effectués sur le site. Chaque couleur a été affichée à 1000 utilisateurs, et voici les résultats :
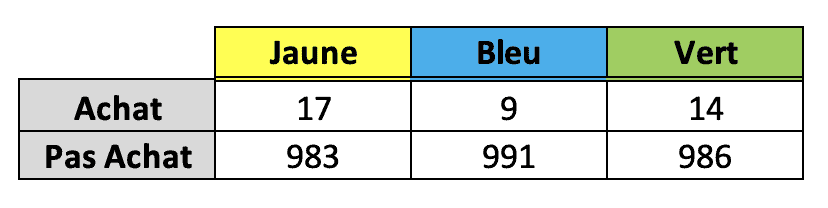
La version jaune semble être presque deux fois meilleure que la version bleue, mais les chiffres sont faibles, alors comment pouvez-vous être sûr que ces résultats ne sont pas dus seulement au hasard ?
C’est là que les Tests d’hypothèses arrivent à la rescousse ! Pour en savoir plus sur le sujet, n’hésitez pas à consulter mon cours…
Permettez-moi de souligner ici le rôle de la distribution du chi carré dans le processus. La première étape consiste à supposer que les trois versions du site Web génèrent le même nombre d’achats, en moyenne. Si cela devait être vrai, nous nous attendons au même nombre d’achats pour chaque version, et ce serait (17+9+14) / 3, ou 13,33 achats. La distribution du chi carré nous permet de mesurer à quel point les achats observés s’écartent de ce qui est attendu si la couleur ne fait aucune différence.
La distribution du Chi carré est utile pour les tests A/B/C. Il mesure la probabilité que les résultats expérimentaux que nous avons obtenus soient le seul résultat du hasard.
Il s’avère que si nous calculons la différence (correctement mise à l’échelle puis au carré) entre les valeurs attendues et observées pour chaque couleur, nous arrivons à une statistique de test qui suit la distribution du chi carré ! Nous pouvons ensuite déduire, en fonction de la valeur p (p-value), si la variation du nombre d’achats que nous avons observés était due au hasard, ou plutôt à la différence de couleur.
Ce test dit du chi-carré se fait en une ligne en Python :
import pandas as pd from scipy.stats import chi2_contingency cont_table = pd.DataFrame([[17, 9, 14], [983, 991, 986]]) chisq, pvalue, df, expected = chi2_contingency(cont_table)
Nous obtenons une valeur de Chi carré (chisq) de 2,48 et la distribution est paramétrée avec 2 degrés de liberté (df). Par conséquent, la distribution en question ressemble à ceci :
df = 2
chi = np.random.chisquare(df, size = 1_000_000)
sns.kdeplot(chi, shade=True, color='xkcd:lightish blue')
plt.title("Distribution du chi-carré avec 2 degrés de liberté")
plt.xlabel('Statistique du Chi-carré')
plt.ylabel('Densité');
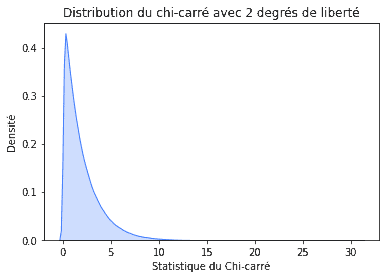
La valeur du chi-carré de 2,48 semble assez probable dans cette distribution, ce qui nous amène à conclure que les différences dans le nombre d’achats pour des sites Web de différentes couleurs peuvent être causées uniquement par le hasard, c’est à dire de façon aléatoire. Ceci est également prouvé par la valeur de p élevée de près de 0,3.
Distribution-F
Revenons sur l’expérience de couleur du site Web, un exemple de test A/B/C. Nous avons évalué l’impact de la couleur sur une variable discrète : le nombre d’achats. Considérons maintenant une variable continue, telle que le nombre de secondes passées, en moyenne, sur chaque variante du site Web.
Dans le cadre de l’expérience, nous avons montré de manière aléatoire aux utilisateurs différentes variantes du site Web et nous avons calculé le temps passé sur le site. Voici les données pour 15 utilisateurs (cinq ont vu la version jaune, cinq autres la bleue, et les cinq derniers la version verte). Pour qu’une telle expérience soit valide, nous aurions besoin de plus de 15 utilisateurs, ce n’est qu’une démonstration.
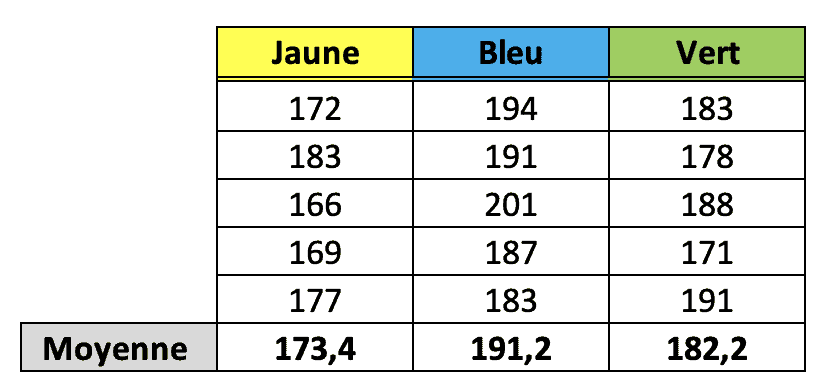
Nous nous intéressons à savoir dans quelle mesure les différences entre les moyennes sont plus grandes que ce qui aurait pu être produit par hasard. Si elles sont significativement plus grandes, alors nous pourrions conclure que la couleur a effectivement un impact sur le temps passé sur le site Web. Une telle comparaison entre les moyennes est appelée ANOVA, ou analyse de la variance.
L’ inférence est assez similaire à celle que nous avons déjà discutée lorsque nous parlons de la distribution du Chi carré. Nous calculons la statistique de test comme étant le rapport entre la variabilité entre les moyennes des groupes et la variation à l’intérieur des groupes. Une telle statistique suit une distribution appelée la distribution F. Sachant cela, nous pouvons utiliser la valeur de p pour rejeter (ou non) l’hypothèse que les moyens sont différents en raison du hasard seul.
La distribution-F est utilisée pour les tests A/B/C lorsque le résultat que nous mesurons est continu.
En Python, nous pouvons exécuter ANOVA en utilisant le paquet statsmodels . Les calculs internes sont basés sur un modèle de régression linéaire, d’où l’appel de ols() et la collecte des données dans un bloc de données à deux colonnes.
import statsmodels.api as sm
import statsmodels.formula.api as smf
websites = pd.DataFrame({
"seconds": [172, 183, 166, 169, 177,
194, 191, 201, 187, 183,
183, 178, 188, 171, 191],
"color": ["y"] * 5 + ["b"] * 5 + ["g"] * 5
})
model = smf.ols("seconds ~ color", data=websites).fit()
anova_table = sm.stats.anova_lm(model)
Et voici la table anova que nous avons obtenu :
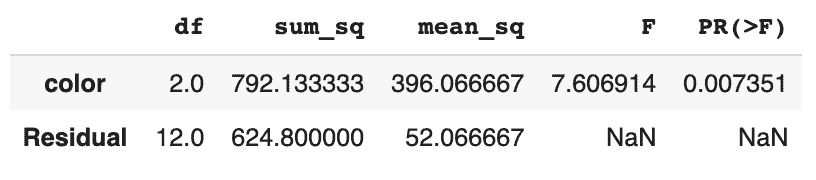
Notre distribution-F est paramétrée avec deux paramètres de degrés de liberté : un pour les différences entre les moyennes de couleur et la moyenne moyenne (2) et un autre pour les différences au sein de chaque couleur (12). Par conséquent, notre distribution se présente comme suit :
df_between = 2
df_within = 12
f = np.random.f(df_between, df_within, size = 1_000_000)
sns.kdeplot(f, shade=True, color='xkcd:lightish blue')
plt.title("Distribution F avec 2 et 12 degrés de liberté")
plt.xlabel('Statistique F')
plt.ylabel('Densité');
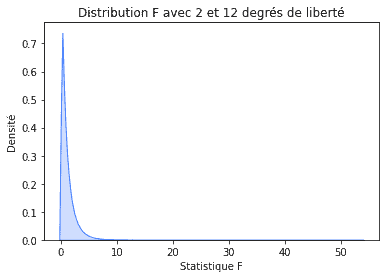
Puisque nous avons obtenu la statistique F égale à 7,6 (et, par conséquent, parce que la valeur de p est faible), nous concluons que la différence entre le temps moyen passé sur différentes variantes du site Web n’aurait pas pu être causée par le hasard. La couleur joue donc bien un rôle ici !
Récap
- La distribution binomiale est utile pour modéliser les données binaires succès / échec. Il peut servir de détecteur d’anomalies ou d’outil pour les tests A/B bayésiens.
- La distribution de Poisson peut être utilisée pour décrire les événements qui se produisent à un certain rythme dans le temps ou l’espace. Il est souvent utilisé pour effectuer des simulations de mise en file d’attente qui aident à allouer des ressources.
- La distribution exponentielle décrit la durée entre deux événements qui suivent la loi de Poisson. Il peut être utilisé comme détecteur d’anomalies ou comme simple référence pour les modèles prédictifs.
- La distribution normale décrit certaines statistiques calculées à partir d’échantillons de données aléatoires, tels qu’établis par le Théorème Central Limite. Grâce à cela, nous pouvons supposer la normalité des erreurs dans les modèles de régression, ou effectuer des tests d’hypothèse facilement.
- La distribution du Chi carré est généralement utilisée pour les tests A/B/C. Il mesure la probabilité que les résultats expérimentaux que nous avons obtenus soient le résultat du hasard seul.
- La distribution-F est utilisée pour les tests A/B/C lorsque le résultat que nous mesurons est continu, par exemple dans l’analyse ANOVA. L’inférence est semblable à celle qui utilise le chi carré pour les résultats discrets.
Pour aller plus loin dans les statistiques orientées sur des applications pratiques et concrètes de Data Science et Business, vous pouvez consulter ce cours en cliquant ici.