T’es tu déjà demandé comment les chiffres peuvent raconter des histoires ? C’est là tout l’intérêt des statistiques : donner un sens aux chiffres pour mieux comprendre les choses.
Considère les statistiques comme l’apprentissage du b.a.-ba de la Data Science. Tu commences par les bases et très vite tu peux analyser des données et faire des prédictions intéressantes !
Dans ce guide facile à suivre, nous allons examiner 20 concepts clés de la statistique. Imagine ces concepts comme les éléments constitutifs de la compréhension des données. Explorons le monde fascinant des statistiques…
#1. Population et échantillon
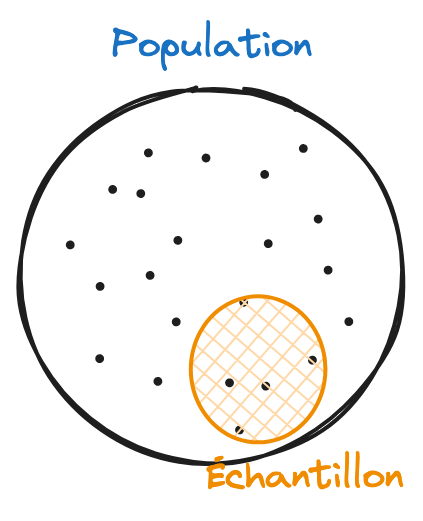
Une population est l’ensemble des individus ou des objets étudiés. Un échantillon est un sous-ensemble de la population utilisé pour faire des déductions sur l’ensemble de la population.
Exemple : Considérons une université de 10 000 étudiants. L’ensemble des 10 000 étudiants représente la population. Si nous sélectionnons 500 étudiants de cette université et analysons leurs habitudes d’étude, ces 500 étudiants constituent l’échantillon.
#2. Statistiques descriptives
Les statistiques descriptives résument et présentent les données de manière significative. Les mesures courantes sont la moyenne, la médiane, le mode, la variance et l’écart-type.
Exemple : Pour un ensemble de données de notes d’examen : Moyenne = 75 (note moyenne), Médiane = 80 (note du milieu), Variance = 100 (dispersion des notes), Écart type = 10 (écart des notes par rapport à la moyenne).
#3. Statistiques inférentielles
La statistique inférentielle consiste à faire des prédictions ou des déductions sur une population à partir d’un échantillon.
Exemple : Nous voulons connaître la taille moyenne de tous les adultes d’un pays. Au lieu de mesurer tout le monde, nous mesurons la taille de 500 adultes (échantillon) et en déduisons la taille moyenne de l’ensemble de la population adulte.
#4. Types de variables
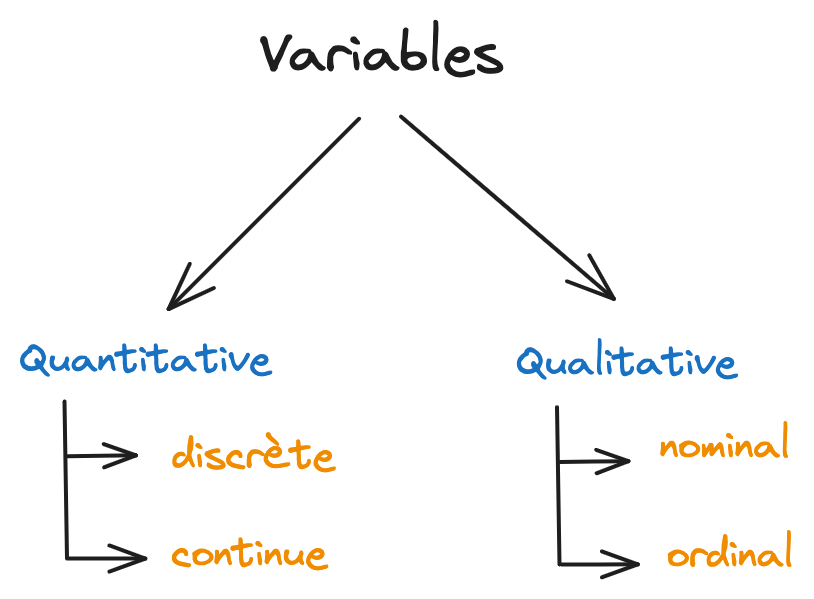
Les variables sont classées en deux catégories : les variables catégorielles (nominales, ordinales) et les variables numériques (discrètes, continues) :
- Nominal : Couleurs (rouge, bleu)
- Ordinal : Variable ayant un certain ordre – Niveaux d’éducation (lycée < licence < master)
- Discrète : Une variable discrète ne peut prendre qu’une valeur entière – Le nombre d’enfants dans une famille.
- Continue : une variable qui peut prendre n’importe quelle valeur flottante – la taille des individus.
#5. Mesures de la tendance centrale
Les mesures telles que la moyenne, la médiane et le mode représentent la tendance centrale d’un ensemble de données.
Exemple : Moyenne de {2, 3, 3, 4, 5} = (2+3+3+4+5)/5 = 3.
Médiane = 3 (valeur du milieu).
Mode = 3 (valeur la plus fréquente).
#6. Mesures de dispersion
Des mesures telles que l’étendue, la variance et l’écart type indiquent le degré de dispersion des données.
Exemple : Pour l’ensemble de données {1, 2, 3, 6, 7}, l’étendue = 7-1 = 6, la variance = 6,25, l’écart type ≈ 2,5.
#7. Corrélation
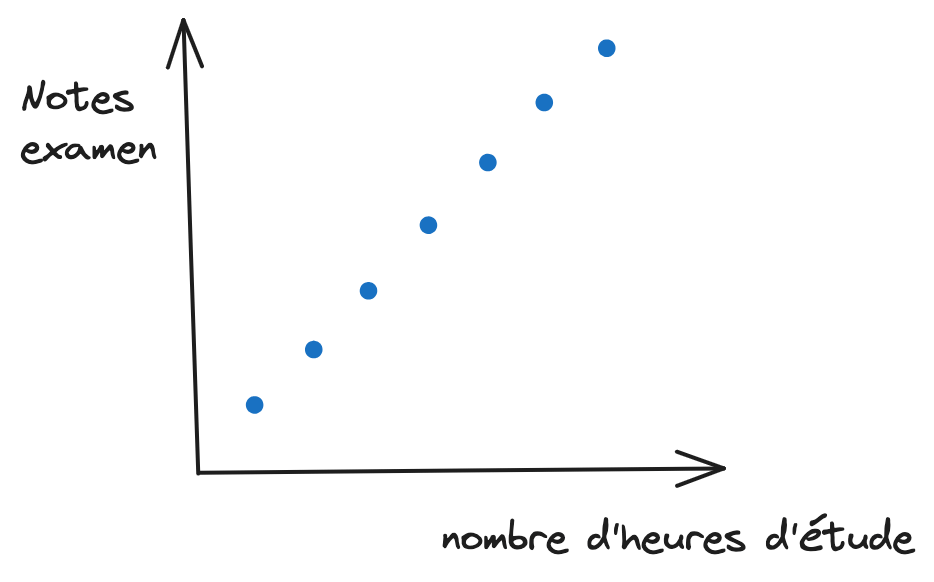
La corrélation mesure la force et la direction d’une relation linéaire entre deux variables.
Exemple : Une étude révèle une forte corrélation positive (0.9) entre le nombre d’heures à étudier et les notes obtenues aux examens, ce qui indique qu’un plus grand nombre d’heures d’étude est associé à de meilleures notes.
#8. Analyse de régression
L’analyse de régression prédit la relation entre une variable dépendante et une ou plusieurs variables indépendantes.
Exemple : Prévoir le prix des maisons en fonction de caractéristiques telles que la superficie, le nombre de chambres et l’emplacement.
#9. Probabilité
La probabilité quantifie l’éventualité qu’un événement se produise, allant de 0 (impossible) à 1 (certain).
Exemple : La probabilité d’obtenir un 6 sur un dé à six faces est de 1/6, soit environ 0,167.
#10. Test d’hypothèse
Le test d’hypothèse évalue la validité d’une affirmation ou d’une hypothèse concernant une population sur la base d’un échantillon de données.
Exemple : Tester l’efficacité d’un nouveau médicament en comparant les taux de guérison d’un groupe traité et d’un groupe non traité.
#11. Z-Score
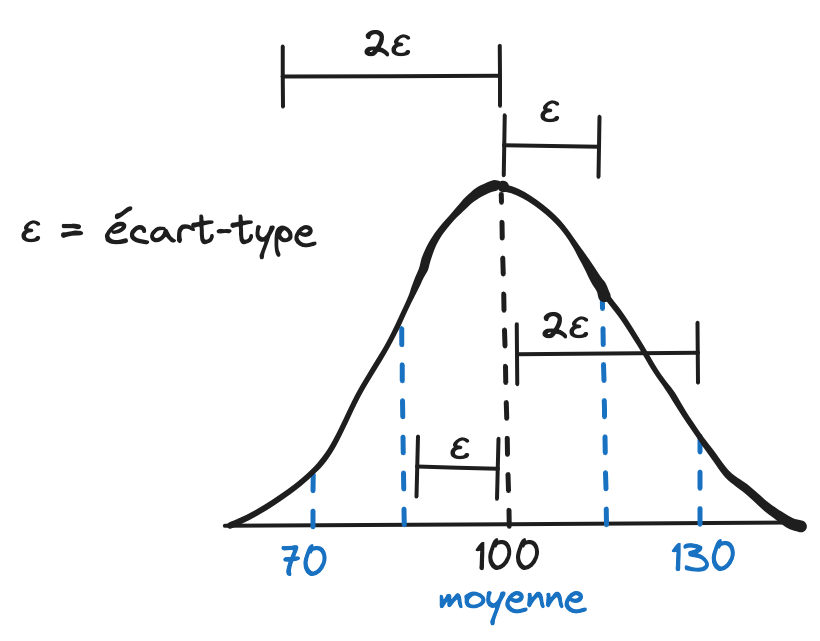
Le Z-score mesure le nombre d’écarts types d’un point de données par rapport à la moyenne, ce qui indique sa position relative dans une distribution.
Exemple : Dans un test de QI avec une moyenne de 100 et un écart-type de 15, un QI de 130 a un Z-score de 2.
#12. Distribution binomiale
Distribution discrète de probabilité du nombre de succès dans une séquence de n expériences indépendantes.
Exemple : En jouant 10 fois à pile ou face avec une pièce de monnaie, la probabilité d’obtenir exactement 7 faces en utilisant la distribution binomiale.
#13. Distribution de Poisson
Une distribution de probabilité discrète qui exprime le nombre d’événements se produisant dans un intervalle de temps ou d’espace fixe.
Exemple : Le nombre d’appels téléphoniques reçus par un centre d’appel en une minute, en supposant un processus de Poisson.
#14. Distribution normale
Distribution symétrique, en forme de cloche, souvent observée dans les phénomènes naturels, avec une moyenne et un écart type définis.
Exemple : La taille des personnes suit souvent une distribution normale dans une population.
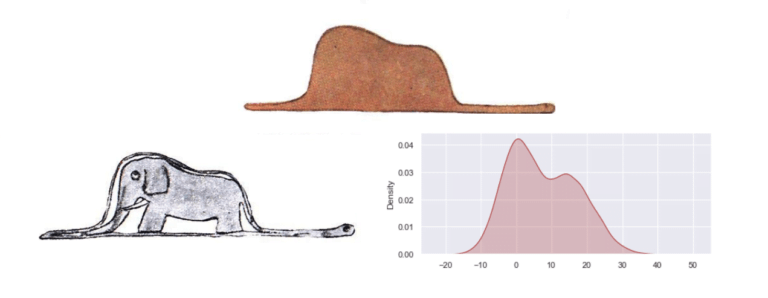
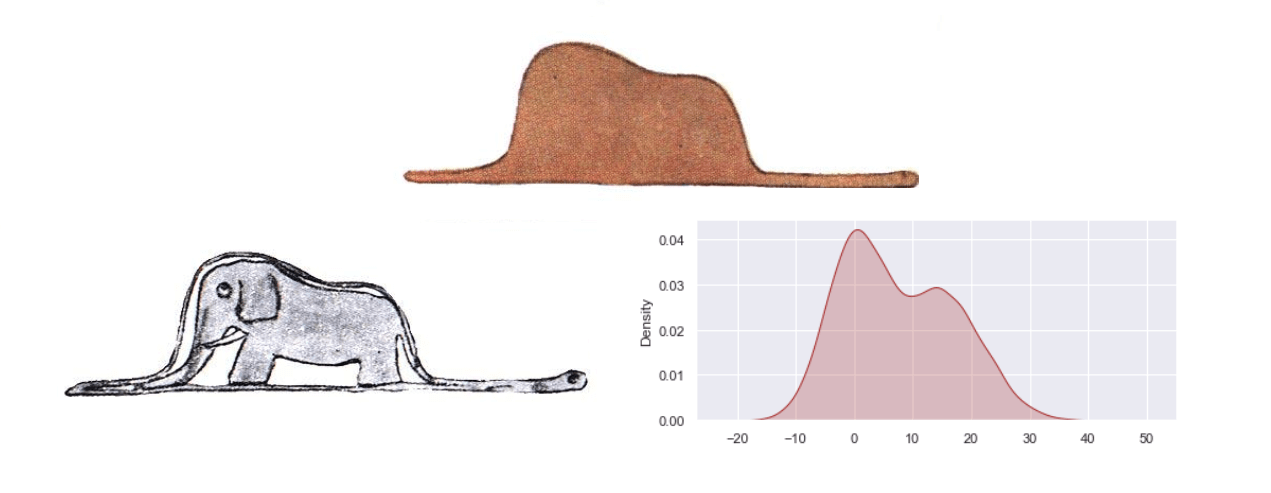
#15. Asymétrie et Kurtosis
L’asymétrie mesure l’asymétrie d’une distribution de probabilité. Le kurtosis mesure la “queue” d’une distribution.
Exemple : Une distribution positivement asymétrique a une queue droite plus longue, comme la distribution des revenus.
#16. Théorème de la limite centrale
Le théorème stipule que, pour un échantillon de taille suffisante, la distribution d’échantillonnage de la moyenne sera approximativement normalement distribuée.
Exemple : Lorsque l’on lance plusieurs fois un dé à six faces et que l’on calcule les moyennes pour chaque série de lancers, la distribution de ces moyennes se rapproche d’une distribution normale à mesure que le nombre de lancers augmente.
#17. Intervalles de confiance
Une plage de valeurs, dérivée des données de l’échantillon, qui est susceptible d’inclure le véritable paramètre inconnu de la population.
Exemple : Estimation d’un intervalle de confiance à 95 % pour la taille moyenne des hommes adultes.
#18. Erreurs de type I et de type II
L’erreur de type I est le rejet d’une hypothèse nulle vraie. L’erreur de type II consiste à ne pas rejeter une hypothèse nulle erronée.
Exemple : Dans un procès, condamner un innocent (type I) ou acquitter un coupable (type II).
#19. ANOVA (analyse de la variance)
L’ANOVA est utilisée pour analyser les différences entre les moyennes des groupes d’un échantillon.
Exemple : Comparaison des notes d’examen d’étudiants ayant suivi trois méthodes d’enseignement différentes.
#20. Test du chi carré
Un test statistique est utilisé pour déterminer s’il existe une association significative entre deux variables catégorielles.
Exemple : Tester l’association entre l’habitude de fumer (oui/non) et les maladies pulmonaires (oui/non).
Conclusion :
Et voilà, c’est terminé ! Félicitations pour avoir suivi ce rapide guide à travers les 20 principaux concepts statistiques. Nous avons abordé de nombreux sujets, de la compréhension des schémas de données à la prise de décision sur la base des nombres.
N’oublie pas que les statistiques t’aident à découvrir des informations et mystères cachés dans tes données. Ces concepts sont les clés qui te permettront d’exploiter la magie des nombres et de les transformer en informations précieuses.
Continue à pratiquer et à expérimenter. Plus tu “joueras” avec ces concepts, plus tu seras à même d’exceller dans les statistiques.