Explorons les algorithmes d’apprentissage automatique (parfait pour les débutants en Data Science). Je t’expliquerai chacun d’entre eux et te montrerai comment les utiliser efficacement.
L’apprentissage automatique (ou Machine Learning) est devenu un outil important dans la boîte à outils du scientifique des données et est devenu un concept célèbre, après avoir vu des applications fantaisistes au cours de la dernière décennie.
Pour exploiter efficacement la puissance de l’apprentissage automatique, il est essentiel de comprendre à la fois les concepts sous-jacents et leurs applications pratiques.
Dans cet article, nous allons explorer les 10 algorithmes d’apprentissage automatique les mieux adaptés à ceux qui débutent dans la science des données, et comment les appliquer.
C’est parti, je t’emmène !
Régression Linéaire
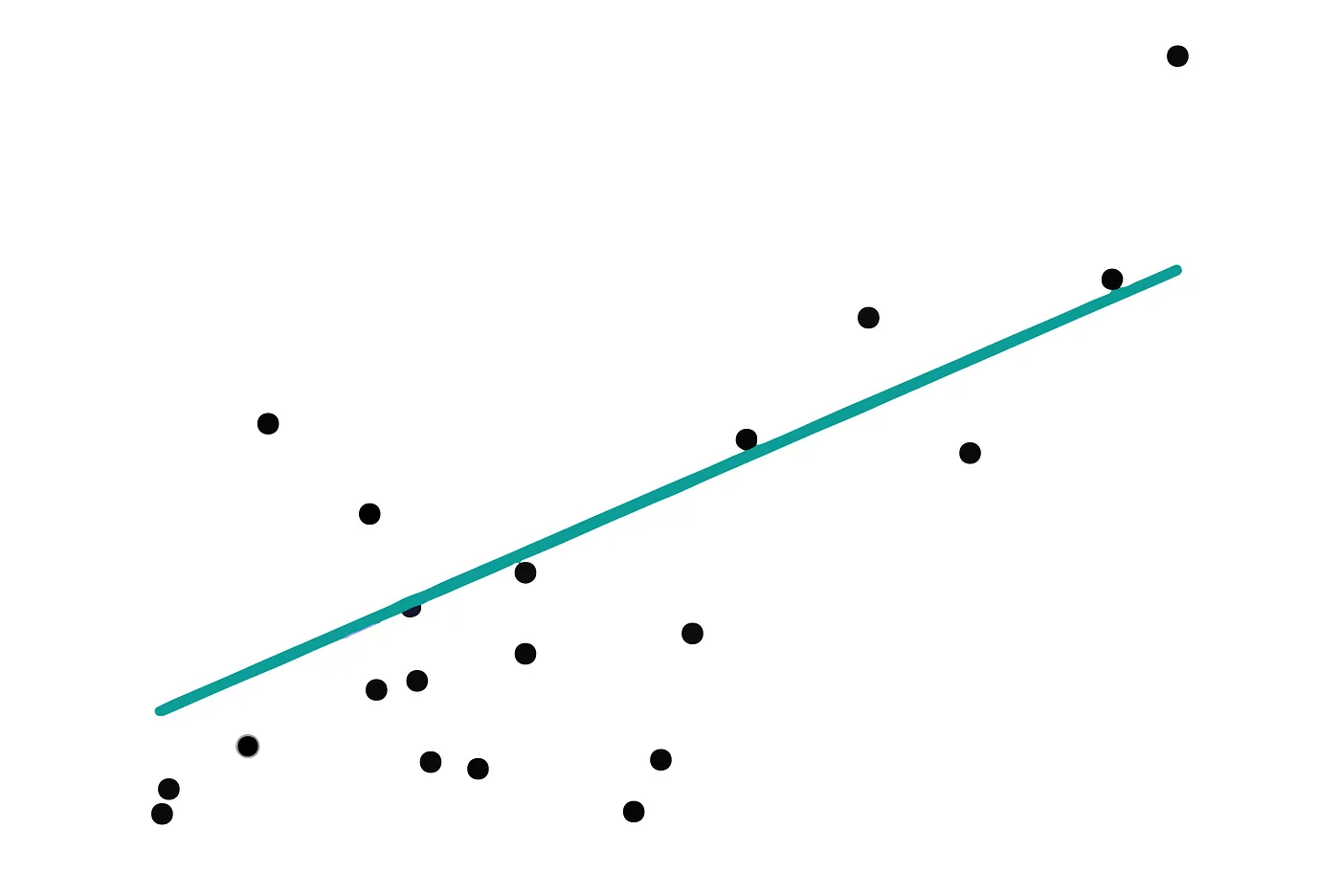
La régression linéaire prédit une sortie continue en établissant une relation linéaire entre les variables d’entrée et la sortie. Imagine que tu traces une ligne droite à travers un ensemble de points sur un graphique.
Il s’agit de trouver la droite qui s’adapte le mieux aux points de données. Cette droite est déterminée en minimisant la différence (erreur) entre les valeurs réelles et les valeurs prédites par la droite de régression.
Métriques d’évaluation
Erreur quadratique moyenne (MSE pour Mean Squared Error) : Mesure la moyenne des carrés des erreurs. Les valeurs les plus faibles sont les meilleures.
R-carré : Représente le pourcentage de la variation de la variable dépendante qui peut être prédite sur la base des variables indépendantes. Une valeur proche de 1 est préférable.
Application avec Scikit-Learn
Puisque nous abordons d’abord la régression linéaire, nous utiliserons l’ensemble de données du diabète, un ensemble de données pré-chargé dans scikit-learn, idéal pour les tâches de régression.
Voici les étapes que nous suivrons dans les blocs de code ci-dessous :
- Charger l’ensemble de données sur le diabète :
Dix variables de base, dont l’âge, le sexe, l’IMC, la pression artérielle moyenne et six mesures de sérum sanguin pour les patients diabétiques, sont incluses dans cet ensemble de données. - Diviser l’ensemble de données :
Divise-le en deux ensembles, l’un pour l’entraînement et l’autre pour le test. - Créer et entraîner le modèle de régression linéaire :
Construis le modèle à l’aide de l’ensemble d’apprentissage (= ensemble d’entraînement). - Prédire et évaluer :
Utilise l’ensemble de test pour faire des prédictions, puis évalue le modèle à l’aide de l’erreur quadratique moyenne (MSE) et du R-carré.
Commençons maintenant !
from sklearn.datasets import load_diabetes
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, r2_score
# Charger l'ensemble de données sur le diabète
diabetes = load_diabetes()
X, y = diabetes.data, diabetes.target
# Division de l'ensemble de données en ensembles d'entraînement et de test
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# Création et entraînement du modèle de régression linéaire
model = LinearRegression()
model.fit(X_train, y_train)
# Prédiction des résultats de l'ensemble de test
y_pred = model.predict(X_test)
# Évaluation du modèle
mse = mean_squared_error(y_test, y_pred)
r2 = r2_score(y_test, y_pred)
print("MSE est de :", mse)
print("R2 score est de :", r2)Voici le résultat :
MSE est de : 2900.193628493482 R2 score est de : 0.4526027629719195
Ces résultats indiquent que notre modèle de régression linéaire explique environ 45 % de la variance dans l’ensemble de données sur le diabète. L’erreur MSE nous indique qu’en moyenne, nos prédictions s’éloignent d’environ 2900 unités des valeurs réelles.
Régression logistique
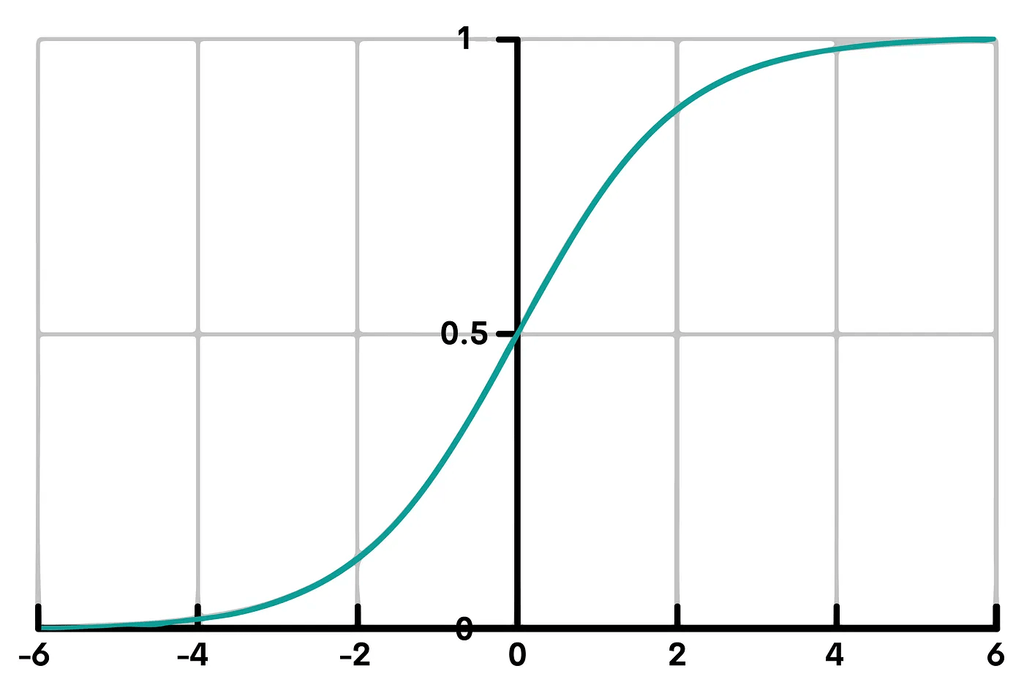
La régression logistique est utilisée pour les problèmes de classification. Elle prédit la probabilité qu’un point de données donné appartienne à une certaine classe, comme oui/non ou 0/1. Elle utilise une fonction logistique pour produire une valeur comprise entre 0 et 1. Cette valeur est ensuite affectée à une classe spécifique sur la base d’un seuil (généralement 0.5).
Métriques d’évaluation
- Accuracy : L’accuracy (exactitude) est le rapport entre les observations correctement prédites et le nombre total d’observations.
- Precision et recall : La précision est le rapport entre les observations positives correctement prédites et toutes les observations positives attendues. Le recall (ou rappel) est la proportion d’observations positives correctement prédites par rapport à toutes les observations effectuées dans la classe réelle.
- Score F1 : Un équilibre entre le recall et la précision.
Application avec Scikit-Learn
L’ensemble de donnéess du cancer du sein, un autre jeu de données pré-chargé dans scikit-learn. Il est utilisé pour la classification binaire, ce qui le rend adapté à la régression logistique.
Voici les étapes à suivre pour appliquer la régression logistique.
- Charger l’ensemble de données du cancer du sein : Cet ensemble de données contient des caractéristiques (ou Features) calculées à partir d’une image numérisée d’une aspiration à l’aiguille fine (AAF) d’une masse mammaire, et l’objectif est de les classer comme bénignes ou malignes.
- Diviser l’ensemble de données : Divise-le en ensembles d’entraînement et de test.
- Créer et entraîner le modèle de régression logistique : Construis le modèle à l’aide de l’ensemble d’apprentissage.
- Prédire et évaluer : Utilise l’ensemble de test pour faire des prédictions, puis évalue le modèle à l’aide de la précision, de l’exactitude, du rappel et du score F1.
Voyons le code :
from sklearn.datasets import load_breast_cancer
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score, precision_score, recall_score, f1_score
# Charger l'ensemble de données sur le cancer du sein
breast_cancer = load_breast_cancer()
X, y = breast_cancer.data, breast_cancer.target
# Division de l'ensemble de données en ensembles d'entraînement et de test
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# Création et entraînement du modèle de régression logistique
model = LogisticRegression(max_iter=10000)
model.fit(X_train, y_train)
# Prédiction des résultats de l'ensemble de tests
y_pred = model.predict(X_test)
# Évaluation du modèle
accuracy = accuracy_score(y_test, y_pred)
precision = precision_score(y_test, y_pred)
recall = recall_score(y_test, y_pred)
f1 = f1_score(y_test, y_pred)
# Impression des résultats
print("Accuracy :", accuracy)
print("Precision :", precision)
print("Recall :", recall)
print("F1 Score :", f1)Voici le résultat :
Accuracy : 0.956140350877193 Precision : 0.9459459459459459 Recall : 0.9859154929577465 F1 Score : 0.9655172413793103
Le taux de rappel (recall) élevé indique que le modèle est particulièrement efficace pour identifier les cas de malignité, ce qui est crucial dans les diagnostics médicaux.
Arbres de décision
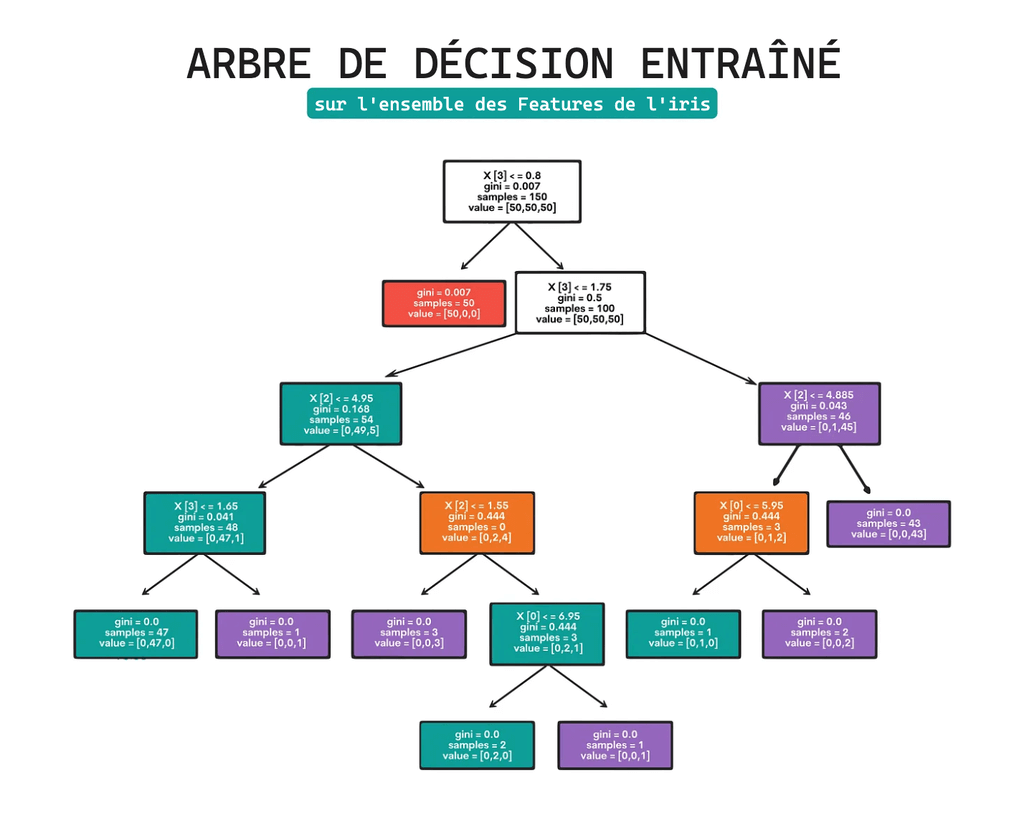
Les arbres de décision (Decision Trees) ressemblent à des organigrammes, divisant les données en fonction de certaines conditions ou caractéristiques. Ils sont appliqués à la régression et à la classification.
Ils fonctionnent en utilisant les valeurs des caractéristiques pour diviser l’ensemble de données en sous-groupes plus faciles à gérer. Chaque nœud interne symbolise un test d’attribut, chaque branche indique le résultat du test et chaque nœud feuille représente une étiquette de classe (décision).
Métriques d’évaluation
- Pour la classification : Precision, accuracy, recall et score F1.
- Pour la régression : Erreur quadratique moyenne (MSE), R-carré.
Application avec Scikit-Learn
Nous utiliserons l’ensemble de données du vin pour les arbres de décision : une tâche de classification. Cet ensemble de données permet de classer les vins en trois types sur la base de différents attributs. Nous allons entraîner le modèle, prédire les types de vins et l’évaluer à l’aide de mesures de classification.
Voici les étapes que nous suivrons dans le code ci-dessous.
- Charger l’ensemble de données sur les vins :
Les analyses chimiques de trois variétés distinctes de vins produits dans la même région d’Italie sont incluses dans l’ensemble de données sur le vin. Treize composants sont identifiés dans des quantités différentes dans chacune des trois catégories de vins par l’étude.
- Diviser l’ensemble de données :
L’ensemble de données comprend des ensembles d’entraînement et de test. Cela permet d’entraîner le modèle sur une partie des données (ensemble d’entraînement) et de tester ses performances sur des données inédites (ensemble de test). Nous avons utilisé 80 % des données pour la formation et 20 % pour le test.
- Créer et entraîner le modèle d’arbre de décision :
Un classificateur d’arbre de décision est créé. Ce modèle apprend à partir des données d’entraînement. Il construit un modèle d’arbre de décisions, où chaque nœud de l’arbre représente une caractéristique de l’ensemble de données, et les branches représentent les règles de décision, conduisant à différents résultats ou classifications.
- Prédire et évaluer :
Le modèle est utilisé pour prédire les classifications de l’ensemble de test. Les performances du modèle sont ensuite évaluées en comparant ces prédictions aux étiquettes réelles.
Voici le code :
from sklearn.datasets import load_wine
from sklearn.tree import DecisionTreeClassifier
# Charger l'ensemble de données sur le vin
wine = load_wine()
X, y = wine.data, wine.target
# Division de l'ensemble de données en ensembles d'entraînement et de test
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# Création et entraînement du modèle d'arbre de décision
model = DecisionTreeClassifier(random_state=42)
model.fit(X_train, y_train)
# Prédiction des résultats de l'ensemble de test
y_pred = model.predict(X_test)
# Évaluation du modèle
accuracy = accuracy_score(y_test, y_pred)
precision = precision_score(y_test, y_pred, average='macro')
recall = recall_score(y_test, y_pred, average='macro')
f1 = f1_score(y_test, y_pred, average='macro')
# Impression des résultats
print("Accuracy :", accuracy)
print("Precision :", precision)
print("Recall :", recall)
print("F1 Score :", f1)Voici le résultat :
Accuracy : 0.9444444444444444 Precision : 0.953968253968254 Recall : 0.9345238095238096 F1 Score : 0.9424740010946907
Ces résultats indiquent que le modèle d’arbre de décision fonctionne très bien sur cet ensemble de données. La précision élevée suggère que lorsqu’il prédit une classe particulière de vin, il est généralement correct.
Naive Bayes
Les “classificateurs de Bayes naïfs” sont une famille de “classificateurs probabilistes” simples qui utilisent le théorème de Bayes et de fortes hypothèses d’indépendance (naïve) entre les caractéristiques. Ils sont particulièrement utilisés pour la classification de textes.
Il calcule la probabilité de chaque classe et la probabilité conditionnelle de chaque classe pour chaque valeur d’entrée. Ces probabilités sont ensuite utilisées pour classer une nouvelle valeur sur la base de la probabilité la plus élevée.
Métriques d’évaluation
- Accuracy : Mesure l’exactitude globale du modèle.
- Precision, recall et score F1 : Particulièrement importants dans les cas où la répartition des classes est déséquilibrée.
Application avec Scikit-Learn
Nous utiliserons l’ensemble de données Digits, qui consiste à classer des images de chiffres manuscrits (0-9). Il s’agit d’un problème de classification multi-classes. Nous allons entraîner le modèle Naive Bayes, prédire les classes de chiffres et l’évaluer à l’aide de mesures de classification. Voici les étapes à suivre.
- Charger l’ensemble de données Digits :
L’ensemble de données Digits se compose d’images de 8×8 pixels de chiffres manuscrits (de 0 à 9). Chaque image est représentée par un vecteur de 64 valeurs (8×8 pixels), chacune représentant l’intensité en niveaux de gris d’un pixel.
- Diviser l’ensemble de données :
Comme dans les exemples précédents, l’ensemble de données est divisé en ensembles d’entraînement et de test. Nous utilisons 80 % des données pour l’entraînement et 20 % pour le test. Cela permet d’entraîner le modèle sur une grande partie des données, puis d’évaluer ses performances sur un autre ensemble qu’il n’a jamais vu auparavant.
- Créer et entraîner le modèle Naive Bayes :
Un classificateur gaussien Naive Bayes est créé. Cette variante de Naive Bayes suppose que les valeurs continues associées à chaque caractéristique sont distribuées selon une distribution gaussienne (normale).
Le modèle est ensuite entraîné (ajusté) sur les données d’apprentissage. Il apprend à associer les caractéristiques d’entrée (valeurs des pixels) aux valeurs cibles (classes de chiffres).
- Prédire et évaluer :
Après l’entraînement, le modèle est utilisé pour prédire les étiquettes de classe des données de test.
Voici le code ci-dessous :
from sklearn.datasets import load_digits
from sklearn.naive_bayes import GaussianNB
# Charger l'ensemble de données Digits
digits = load_digits()
X, y = digits.data, digits.target
# Division de l'ensemble de données en ensembles d'entraînement et de test
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# Création et entraînement du modèle Naive Bayes
model = GaussianNB()
model.fit(X_train, y_train)
# Prédiction des résultats de l'ensemble de tests
y_pred = model.predict(X_test)
# Évaluation du modèle
accuracy = accuracy_score(y_test, y_pred)
precision = precision_score(y_test, y_pred, average='macro')
recall = recall_score(y_test, y_pred, average='macro')
f1 = f1_score(y_test, y_pred, average='macro')
# Impression des résultats
print("Accuracy :", accuracy)
print("Precision :", precision)
print("Recall :", recall)
print("F1 Score :", f1)Voici le résultat :
Accuracy : 0.8472222222222222 Precision : 0.8649844547206135 Recall : 0.8476479221745045 F1 Score : 0.8437352605469787
Ces résultats montrent que le modèle Naive Bayes a de bonnes performances sur cet ensemble de données, avec une précision et un rappel relativement équilibrés. Le modèle est assez efficace pour classer les chiffres manuscrits, même s’il peut être amélioré, en particulier en termes d’accuracy et de score F1.
K-Nearest Neighbors (KNN)
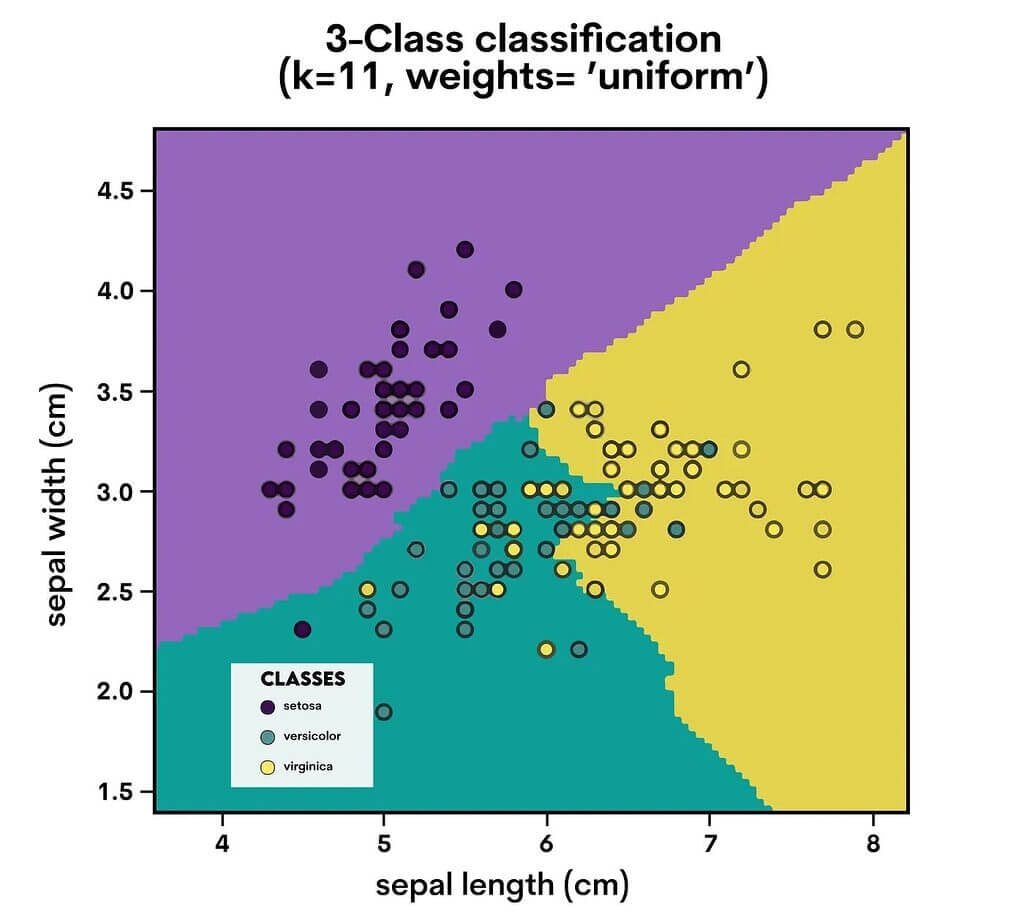
Une approche facile à comprendre pour la régression et la classification est celle des K-voisins les plus proches (KNN). Un point de données est classé en fonction de la classification de ses voisins.
KNN examine les “K” points les plus proches (voisins) d’un point de données et le classe en fonction de la classe majoritaire de ces voisins. Pour la régression, il prend la moyenne des “K” points les plus proches.
Métriques d’évaluation
- Classification : Precision, accuracy, recall, score F1.
- Régression : Erreur quadratique moyenne (ME), R-carré.
Application avec Scikit-Learn
Nous utiliserons à nouveau l’ensemble de données sur le vin, mais cette fois-ci avec KNN. Nous allons entraîner le modèle KNN à classer les types de vin et évaluer ses performances à l’aide de métriques de classification. Voici les étapes à suivre :
- Créer et entraîner le modèle KNN :
Un modèle KNN (K-Nearest Neighbors) est créé avec n_neighbors=3. Cela signifie que le modèle considère les trois voisins les plus proches d’un point de données pour faire une prédiction.
Le modèle est formé (ajusté) avec les données d’apprentissage. Pendant l’entraînement, il ne construit pas un modèle traditionnel mais mémorise l’ensemble des données. - Prédiction :
Le modèle KNN entraîné est ensuite utilisé pour prédire les étiquettes de classe (types de vin) des données de test. Le modèle détermine la classe la plus courante parmi ces voisins pour chaque point de l’ensemble de test en examinant les trois points les plus proches dans l’ensemble d’entraînement. - Évaluation :
Les prédictions du modèle sont évaluées par rapport aux étiquettes réelles de l’ensemble de test.
Voici le code :
from sklearn.datasets import load_wine
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsClassifier
from sklearn.metrics import accuracy_score, precision_score, recall_score, f1_score
# Charger l'ensemble de données sur le vin
wine = load_wine()
X, y = wine.data, wine.target
# Division de l'ensemble de données en ensembles d'entraînement et de test
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# Création et entraînement du modèle KNN
knn_model = KNeighborsClassifier(n_neighbors=3)
knn_model.fit(X_train, y_train)
# Prédiction des résultats de l'ensemble de test
y_pred_knn = knn_model.predict(X_test)
# Évaluation du modèle
accuracy_knn = accuracy_score(y_test, y_pred_knn)
precision_knn = precision_score(y_test, y_pred_knn, average='macro')
recall_knn = recall_score(y_test, y_pred_knn, average='macro')
f1_knn = f1_score(y_test, y_pred_knn, average='macro')
# Impression des résultats
print("Accuracy :", accuracy_knn)
print("Precision :", precision_knn)
print("Recall :", recall_knn)
print("F1 Score :", f1_knn)Voici le résultat :
Accuracy : 0.8055555555555556 Precision : 0.7912698412698412 Recall : 0.7976190476190476 F1 Score : 0.7899877899877898
Ces résultats indiquent que le modèle KNN est exceptionnellement performant sur cet ensemble de données. Les scores élevés de toutes les mesures montrent que le modèle est non seulement précis dans l’ensemble, mais qu’il maintient également un bon équilibre entre la précision et le rappel, ce qui permet de classer efficacement les types de vin.
Support Vector Machines (SVM)
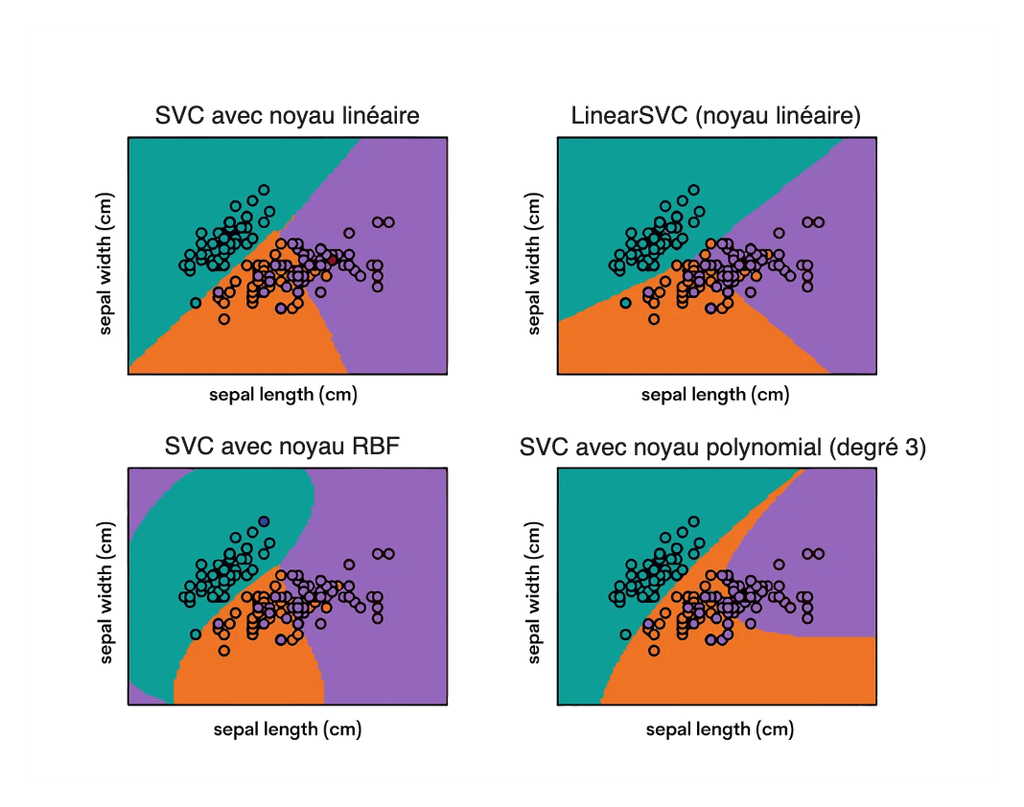
Les machines à vecteurs de support (SVM) sont des modèles d’apprentissage supervisé puissants et polyvalents, utilisés pour les tâches de classification et de régression. Ils fonctionnent bien pour les ensembles de données complexes.
Les SVM construisent un hyperplan (ou un ensemble d’hyperplans) dans un espace à haute dimension pour séparer les différentes classes. Il vise à trouver la meilleure marge (distance entre la ligne et les points les plus proches de chaque classe, appelés vecteurs de support) qui sépare les classes.
Métriques d’évaluation
- Classification : Precision, accuracy, recall, score F1.
- Régression : Erreur quadratique moyenne (MSE), R-carré.
Application avec Scikit-Learn
Nous appliquerons le SVM à l’ensemble de données sur le cancer du sein, en nous concentrant sur la classification des tumeurs comme bénignes ou malignes. Nous entraînerons le modèle SVM et évaluerons ses performances à l’aide de mesures de classification.
Voici les étapes à suivre :
- Créer et entraîner le modèle SVM :
Un modèle de machine à vecteur de support (SVM) est créé en utilisant les paramètres par défaut. Les SVM sont connus pour leur capacité à créer un hyperplan (ou plusieurs hyperplans dans des espaces de dimension supérieure) qui sépare les classes avec une marge aussi grande que possible.
- Prédire :
Le modèle SVM entraîné est ensuite utilisé pour prédire les étiquettes de classe des données de test. Pour ce faire, il détermine de quel côté de l’hyperplan se situe chaque point de données.
- Évaluer :
- Les prédictions du modèle sont évaluées par rapport aux étiquettes réelles de l’ensemble de test afin d’évaluer ses performances.
Voici le code :
from sklearn.svm import SVC
breast_cancer = load_breast_cancer()
X, y = breast_cancer.data, breast_cancer.target
# Division de l'ensemble de données en ensembles d'entraînement et de test
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# Création et entraînement du modèle SVM
svm_model = SVC()
svm_model.fit(X_train, y_train)
# Prédiction des résultats de l'ensemble de tests
y_pred_svm = svm_model.predict(X_test)
# Évaluation du modèle
accuracy_svm = accuracy_score(y_test, y_pred_svm)
precision_svm = precision_score(y_test, y_pred_svm, average='macro')
recall_svm = recall_score(y_test, y_pred_svm, average='macro')
f1_svm = f1_score(y_test, y_pred_svm, average='macro')
accuracy_svm, precision_svm, recall_svm, f1_svm
# Impression des résultats
print("Accuracy :", accuracy_svm)
print("Precision :", precision_svm)
print("Recall :", recall_svm)
print("F1 Score :", f1_svm)Voici le résultat :
Accuracy : 0.9473684210526315 Precision : 0.961038961038961 Recall : 0.9302325581395349 F1 Score : 0.9422297297297297
Ces résultats indiquent que le modèle SVM est exceptionnellement performant sur l’ensemble de données du cancer du sein. Les scores élevés d’exactitude, de précision, de rappel et de F1 démontrent l’efficacité du modèle à distinguer les tumeurs bénignes des tumeurs malignes.
L’équilibre entre la précision et le rappel est particulièrement important dans les diagnostics médicaux, où les faux positifs et les faux négatifs ont des conséquences importantes.
Random Forest
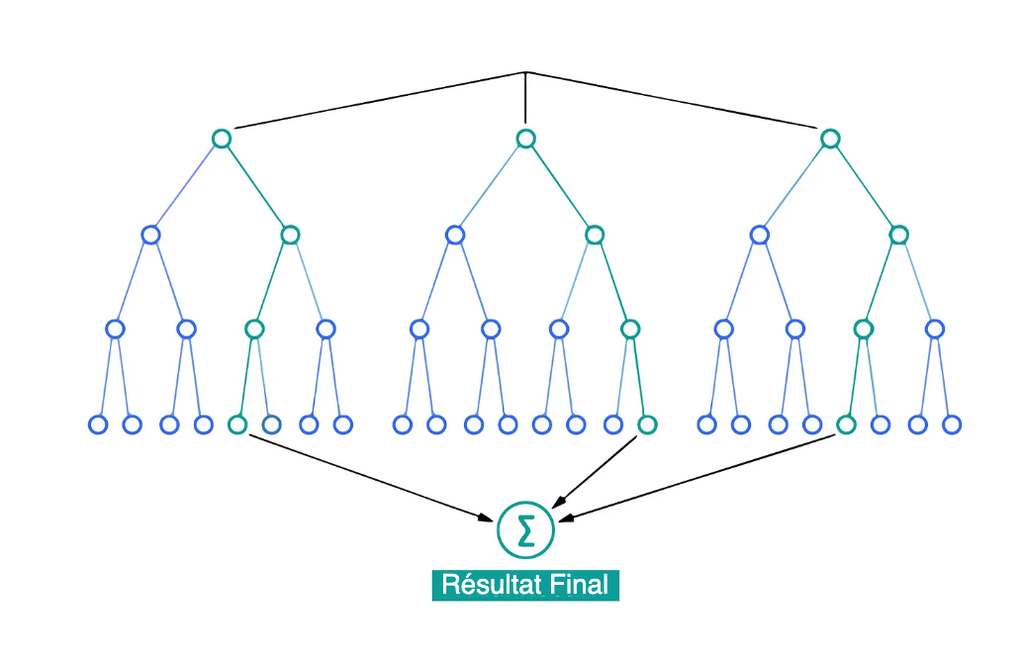
Une technique d’apprentissage ensembliste généralement utilisée pour la régression et la classification est appelée Random Forest. Pour fournir une prévision plus fiable et plus précise, elle construit de nombreux arbres de décision et les mélange.
Chaque arbre d’une forêt aléatoire émet une prévision et la prédiction du modèle (pour la classification) appartient à la classe qui reçoit le plus de votes. Pour la régression, il s’agit de la moyenne des résultats des différents arbres.
Métriques d’évaluation
- Classification : Precision, accuracy, recall, score F1.
- Régression : Erreur quadratique moyenne (MSE), R-carré.
Application avec Scikit-Learn
Nous appliquerons Random Forest à l’ensemble de données sur le cancer du sein pour classer les tumeurs comme bénignes ou malignes. Nous formerons le modèle Random Forest et évaluerons ses performances à l’aide de mesures de classification.
- Créer et entraîner le modèle Random Forest :
Initialise un classificateur de Random Forest.
En utilisant les données d’entraînement, ajuster (entraîner) le modèle. - Prédire :
Utilise le modèle entraîné pour prédire les étiquettes des données de test. - Évaluer :
Évalue les performances du modèle sur les données de test à l’aide des paramètres Accuracy, Precision, Recall et F1 Score.
Voyons le code :
from sklearn.ensemble import RandomForestClassifier
breast_cancer = load_breast_cancer()
X, y = breast_cancer.data, breast_cancer.target
# Division de l'ensemble de données en ensembles d'entraînement et de test
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# Création et entraînement du modèle Random Forest
rf_model = RandomForestClassifier(random_state=42)
rf_model.fit(X_train, y_train)
# Prédiction des résultats de l'ensemble de test
y_pred_rf = rf_model.predict(X_test)
# Évaluation du modèle
accuracy_rf = accuracy_score(y_test, y_pred_rf)
precision_rf = precision_score(y_test, y_pred_rf, average='macro')
recall_rf = recall_score(y_test, y_pred_rf, average='macro')
f1_rf = f1_score(y_test, y_pred_rf, average='macro')
# Impression des résultats
print("Accuracy :", accuracy)
print("Precision :", precision)
print("Recall :", recall)
print("F1 Score :", f1)Voici le résultat :
Accuracy : 0.9649122807017544 Precision : 0.9672569328433009 Recall : 0.9580740255486406 F1 Score : 0.9623015873015873
Ces résultats démontrent que le modèle Random Forest a un haut niveau de performance sur l’ensemble de données du cancer du sein, avec des scores élevés pour toutes les mesures clés.
La précision et le rappel élevés suggèrent que le modèle est efficace pour identifier avec précision les tumeurs bénignes et malignes, avec une approche équilibrée pour minimiser à la fois les faux positifs et les faux négatifs.
K-Means Clustering
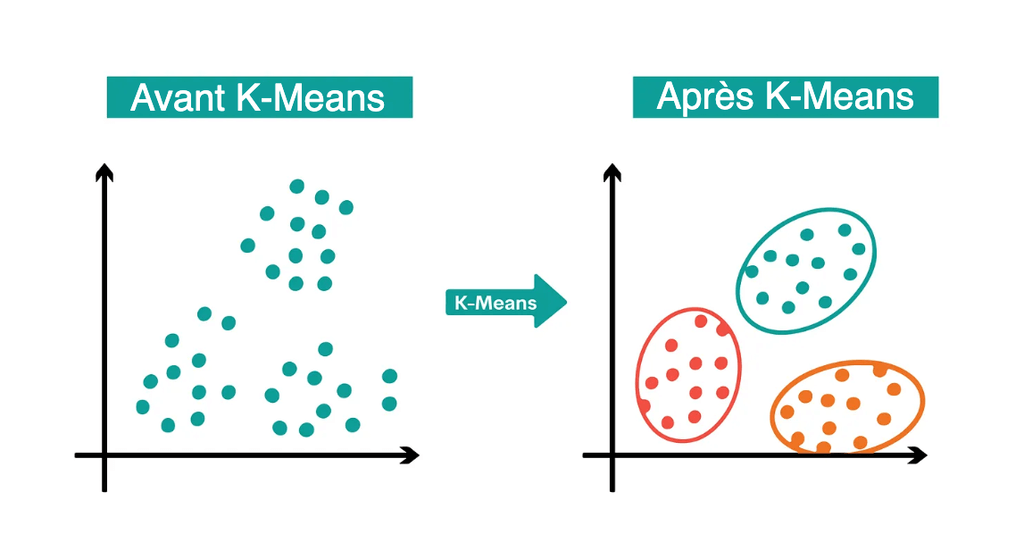
Le K-Means Clustering est un algorithme d’apprentissage non supervisé utilisé pour regrouper les données en “K” cludsters. Après l’identification de k centroïdes, chaque point de données est assigné au cluster le plus proche dans le but de minimiser la taille des centroïdes.
L’algorithme affecte les points de données à un cluster de telle sorte que la somme des carrés de la distance entre les points de données et le centroïde du cluster soit minimale. L’homogénéité des points de données à l’intérieur d’un cluster augmente avec la diminution de la variance à l’intérieur du cluster.
Métriques d’évaluation
- Inertie : la distance totale au carré des échantillons par rapport au centre du cluster le plus proche est appelée inertie. Il est préférable d’avoir des valeurs plus faibles.
- Score de silhouette : indique le degré de cohésion d’un élément par rapport à son appartenance à son propre cluster, par opposition au degré de séparation par rapport aux autres clusters. Un score de silhouette élevé signifie que l’élément est bien assorti à son propre cluster et mal assorti aux clusters voisins. Le score de silhouette va de -1 à 1.
Application avec Scikit-Learn
Utilisons l’ensemble de données Iris pour le K-Means Clustering. La tâche consistera à regrouper les plants d’iris en clusters sur la base des mesures de leurs fleurs. Nous allons entraîner le modèle, assigner les plantes aux clusters et évaluer le clustering.
- Charger l’ensemble de données Iris :
L’ensemble de données Iris contient des mesures de fleurs d’iris, notamment la longueur et la largeur des sépales, la longueur et la largeur des pétales. L’ensemble de données est généralement utilisé pour des tâches de classification, mais ici, nous l’utiliserons pour le clustering.
- Appliquer le K-Means Clustering :
Nous initialisons un algorithme de K-Means Clustering avec n_clusters=3, car il y a trois espèces d’iris dans l’ensemble de données. Cependant, l’algorithme ne connaît pas ces espèces ; il essaiera simplement de trouver la meilleure façon de regrouper les données en trois clusters.
Nous adaptons le modèle aux données X, qui comprennent nos quatre caractéristiques. L’algorithme K-Means assigne itérativement chaque point de données à l’un des trois clusters en fonction de la distance entre le point de données et les centroïdes du cluster. - Prédire les Clusters :
La méthode de prédiction est utilisée pour affecter chaque point de données dans X à l’une des trois clusters. Cette étape est quelque peu conceptuelle avec K-Means puisque l’ajustement et la prédiction ont lieu ensemble, mais essentiellement, chaque point de données est maintenant étiqueté avec un numéro de cluster. - Évaluer le Clustering :
Nous évaluons notre clustering à l’aide de deux mesures :
– Inertie : il s’agit de la somme des distances au carré des échantillons par rapport à leur centre de cluster le plus proche. Il s’agit d’une mesure de la cohérence interne des clusters. Nous visons une inertie faible.
– Score de silhouette : Il s’agit d’une mesure de la similarité d’un objet avec son propre cluster (cohésion) par rapport aux autres clusters (séparation). Le score de silhouette est compris entre -1 et 1. Une valeur élevée indique que l’objet est bien assorti à son propre cluster et mal assorti aux clusters voisins.
Voyons le code :
from sklearn.datasets import load_iris
from sklearn.cluster import KMeans
from sklearn.metrics import silhouette_score
# Charger l'ensemble de données Iris
iris = load_iris()
X = iris.data
# Application du K-Means Clustering
kmeans = KMeans(n_clusters=3, random_state=42)
kmeans.fit(X)
# Prédiction du cluster pour chaque point de données
y_pred_clusters = kmeans.predict(X)
# Évaluation du modèle
inertia = kmeans.inertia_
silhouette = silhouette_score(X, y_pred_clusters)
print("Inertie :", inertia)
print("Silhouette :", silhouette)Voici le résultat :
Inertie : 78.85144142614601 Silhouette : 0.5528190123564095
Ces mesures suggèrent que l’algorithme K-Means a raisonnablement bien fonctionné pour le regroupement de l’ensemble de données Iris, bien qu’il y ait une marge d’amélioration en termes de compacité et de séparation des clusters.
Analyse en Composantes Principales (PCA)
La réduction de la dimensionnalité est réalisée par l’utilisation de l’analyse en composantes principales (Principal Component Analysis – PCA). Elle transforme les données dans un nouveau système de coordonnées, réduisant le nombre de variables tout en préservant autant que possible la variation des données d’origine.
Le PCA permet de trouver les composantes principales, ou axes, qui maximisent la variance des données. La première composante principale capte la plus grande variance, la deuxième composante principale (orthogonale à la première) capte la plus grande variance suivante, et ainsi de suite.
Métriques d’évaluation
- Variance expliquée : Indique la part de variance des données capturée par chaque composante principale.
- Variance totale expliquée : Variance cumulative expliquée par les composantes principales sélectionnées.
Application avec Scikit-Learn
L’ensemble de données sur le cancer du sein, qui comprend des caractéristiques dérivées d’une image numérique d’une aspiration à l’aiguille fine (AAF) d’une tumeur du sein, sera soumis au PCA. Notre objectif est de minimiser la dimensionnalité de l’ensemble de données tout en conservant la plus grande quantité d’informations.
Voici les étapes à suivre :
- Charger l’ensemble de données sur le cancer du sein :
L’ensemble de données sur le cancer du sein se compose de caractéristiques calculées à partir d’images numérisées d’aspirations à l’aiguille fine de masses mammaires. Les caractéristiques sont des attributs des noyaux cellulaires visibles sur l’image.
- Appliquer le PCA :
Nous initialisons l’ACP avec n_components=2, ce qui indique notre intention de réduire l’ensemble de données à deux dimensions. Ce choix est souvent fait à des fins de visualisation ou comme étape de pré-traitement pour d’autres algorithmes.
Nous adaptons le PCA aux données X. Au cours de ce processus, le PCA identifie les axes (composantes principales) qui représentent la plus grande variance dans les données. - Transformer les données :
La méthode de transformation du PCA est utilisée pour appliquer la réduction de la dimensionnalité à X. Il en résulte un nouvel ensemble de données X_pca, où chaque point de données est désormais représenté en fonction des deux composantes principales. - Évaluer la transformation PCA :
Nous évaluons notre transformation PCA en examinant la variance expliquée de chaque composante principale. Cela nous indique quelle part de la variance totale des données est capturée par chaque composante principale.
La variance totale expliquée est calculée en additionnant les variances expliquées des deux composantes principales. Cela nous donne une mesure globale de la quantité d’informations préservées lors du processus de réduction de la dimensionnalité.
Voyons maintenant le code :
from sklearn.datasets import load_breast_cancer
from sklearn.decomposition import PCA
import numpy as np
# Charger l'ensemble de données sur le cancer du sein
breast_cancer = load_breast_cancer()
X = breast_cancer.data
# Application du PCA
pca = PCA(n_components=2) # Réduire à 2 dimensions pour plus de simplicité
pca.fit(X)
# Transformation des données
X_pca = pca.transform(X)
# Variance expliquée
explained_variance = pca.explained_variance_ratio_
# Variance totale expliquée
total_explained_variance = np.sum(explained_variance)
print("Variance expliquée :", explained_variance)
print("Variance totale expliquée :", total_explained_variance)Voyons voir le résultat :
Variance expliquée : [0.98204467 0.01617649] Variance totale expliquée : 0.9982211613741728
Évaluons les résultats.
Variance expliquée :
- Première composante principale : 98,20
- Deuxième composante principale : 1,62%.
- Variance totale expliquée : 99,82 %.
Ces résultats indiquent qu’en réduisant l’ensemble de données à seulement deux composantes principales, nous avons capturé environ 99,82 % de la variance totale de l’ensemble de données.
La première composante explique à elle seule une grande partie de cette variance, ce qui suggère qu’elle capture la plupart des informations essentielles présentes dans l’ensemble de données.
Algorithmes de Gradient Boosting
Le Gradient Boosting est une technique avancée d’apprentissage automatique. Elle permet de construire plusieurs modèles prédictifs faibles (généralement des arbres de décision) de manière séquentielle. Chaque nouveau modèle minimise progressivement la fonction de perte (erreur) de l’ensemble du système.
Trois composants sont impliqués : un modèle additif qui ajoute des apprenants faibles pour minimiser la fonction de perte, une fonction de perte qui doit être optimisée et un apprenant faible qui doit générer des prédictions. Chaque nouvel arbre corrige les erreurs commises par les arbres précédents.
Métriques d’évaluation
- Pour la classification : Precision, Accuracy, Recall, F1 Score.
- Pour la régression : Erreur quadratique moyenne (MSE), R-carré.
APPLICATION AVEC SCIKIT-LEARN
Nous utiliserons l’ensemble de données du Diabète pour le Gradient Boosting. Notre objectif sera de prédire la progression du diabète en fonction de diverses caractéristiques. Nous allons entraîner un modèle de gradient-boosting et évaluer ses performances.
Voyons les étapes à suivre ci-dessous :
- Charger l’ensemble de données sur le diabète
L’âge, le sexe, l’indice de masse corporelle, la pression artérielle moyenne et six mesures de sérum sanguin font partie des caractéristiques incluses dans l’ensemble de données sur le diabète. Un an après la ligne de base, une évaluation quantitative de l’évolution de la maladie est la variable cible.
- Créer et entraîner le modèle de Gradient Boosting :
Nous initialisons un régresseur de stimulation de gradient. Le Gradient Boosting permet d’optimiser n’importe quelle fonction de perte différentiable et de construire un modèle additif en avançant pas à pas.
Nous entraînons (ajustons) ce modèle sur les données d’apprentissage. Au cours de cette étape, le modèle apprend à prédire l’évolution du diabète sur la base des caractéristiques.
- Prédire :
Nous utilisons le modèle de Graadient Boosting entraîné pour prédire l’évolution de la maladie sur les données de test. Cette étape consiste à appliquer le modèle à des données inédites afin d’évaluer ses capacités de prédiction. - Évaluer :
Les performances du modèle sont évaluées à l’aide de deux mesures clés :
– Erreur quadratique moyenne (MSE) : Cette mesure calcule la moyenne des carrés des erreurs. Il s’agit d’une mesure permettant d’évaluer la qualité d’un estimateur ; les valeurs proches de zéro indiquent une meilleure qualité.
– R-carré : Basée sur le pourcentage de la variance totale des résultats que le modèle explique, cette statistique donne une indication de la manière dont les résultats observés sont reproduits par le modèle.
Voici le code :
from sklearn.datasets import load_diabetes
from sklearn.ensemble import GradientBoostingRegressor
from sklearn.metrics import mean_squared_error, r2_score
# Charger l'ensemble de données sur le diabète
diabetes = load_diabetes()
X, y = diabetes.data, diabetes.target
# Division de l'ensemble de données en ensembles d'entraînement et de test
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# Création et entraînement du modèle Gradient Boosting
gb_model = GradientBoostingRegressor(random_state=42)
gb_model.fit(X_train, y_train)
# Prédiction des résultats de l'ensemble de test
y_pred_gb = gb_model.predict(X_test)
# Évaluation du modèle
mse_gb = mean_squared_error(y_test, y_pred_gb)
r2_gb = r2_score(y_test, y_pred_gb)
print("MSE :", mse_gb)
print("Score R2 :", r2_gb)Voici le résultat :
MSE : 2898.4366729135227 Score R2 : 0.4529343796683364
Ces résultats indiquent que le modèle de gradient-boosting a un niveau modéré de précision dans la prédiction de la progression du diabète.
La valeur R-carré de 0.45 suggère que près de 45 % de la variance de la variable cible est expliquée par le modèle, ce qui est satisfaisant pour une tâche complexe comme celle-ci.
L’erreur MSE nous donne une idée de la différence moyenne au carré entre les résultats réels observés et les résultats prédits par le modèle.
Réflexions finales
Dans cet article, nous avons passé en revue les 10 principaux algorithmes d’apprentissage automatique indispensables à tout data scientist en herbe.
N’oublie pas que la maîtrise de ces algorithmes passe par une pratique et une application constantes dans des scénarios réels.