J’éprouve une grande admiration pour la bibliothèque NumPy. C’est pourquoi j’ai toujours mis beaucoup d’énergie pour devenir un ninja de NumPy.
Pourquoi ne pas en faire profiter tout le monde ?
Me voici donc avec une liste des fonctions NumPy les plus cool et les plus rares qui, une fois utilisées, rendront certainement ton code beaucoup plus élégant.
Avant d’apprécier ma liste des 20 astuces NumPy les plus élégantes, tu peux recevoir directement dans ta boîte mail mon top 50 des fonctions NumPy.
1. np.full_like
Je parie que tu as déjà utilisé des fonctions NumPy standard telles que ones_like ou zeros_like à de nombreuses reprises. Eh bien, full_like est exactement comme ces deux fonctions, sauf que tu peux créer une matrice ayant la même forme qu’une autre, remplie avec une valeur personnalisée.
array = np.array([[1, 4, 6, 8], [9, 4, 4, 4], [2, 7, 2, 3]])
array_w_inf = np.full_like(array, fill_value=np.pi, dtype=np.float32)
>>> array_w_inf
array([[3.1415927, 3.1415927, 3.1415927, 3.1415927],
[3.1415927, 3.1415927, 3.1415927, 3.1415927],
[3.1415927, 3.1415927, 3.1415927, 3.1415927]], dtype=float32)Ici, nous créons une matrice de pi, avec la forme de array.
Documentation de full_like.
2. np.logspace
Je suis sûr que tu utilises régulièrement linspace. Il permet de créer un nombre personnalisé de points de données linéairement espacés dans un intervalle. Son cousin logspace va un peu plus loin. Il permet de générer un nombre personnalisé de points régulièrement espacés sur une échelle logarithmique. Tu peux choisir n’importe quel nombre comme base, à condition qu’il ne soit pas nul :
log_array = np.logspace(start=1, stop=100, num=15, base=np.e)
>>> log_array
array([2.71828183e+00, 3.20167238e+03, 3.77102401e+06, 4.44162312e+09,
5.23147450e+12, 6.16178472e+15, 7.25753148e+18, 8.54813429e+21,
1.00682443e+25, 1.18586746e+28, 1.39674961e+31, 1.64513282e+34,
1.93768588e+37, 2.28226349e+40, 2.68811714e+43])Documentation de logspace.
3. np.meshgrid
Il s’agit d’une de ces fonctions que l’on ne voit que dans les documentations. Pendant un certain temps, j’ai pensé qu’elle n’était pas destinée à un usage public parce que j’avais beaucoup de mal à la comprendre.
Et bien, comme toujours, StackOverflow est à la rescousse. D’après ce thread, tu peux créer toutes les paires de coordonnées possibles à partir d’un tableau X et Y donné en utilisant maigri. En voici un exemple simple :
x = [1, 2, 3, 4]
y = [3, 5, 6, 8]
xx, yy = np.meshgrid(x, y)
>>> xx
array([[1, 2, 3, 4],
[1, 2, 3, 4],
[1, 2, 3, 4],
[1, 2, 3, 4]])
>>> yy
array([[3, 3, 3, 3],
[5, 5, 5, 5],
[6, 6, 6, 6],
[8, 8, 8, 8]])Il y aura 16 paires de coordonnées uniques, une pour chaque paire d’éléments d’index à index dans les tableaux résultants.
>>> plt.plot(xx, yy, linestyle="none", marker="o", color="red");
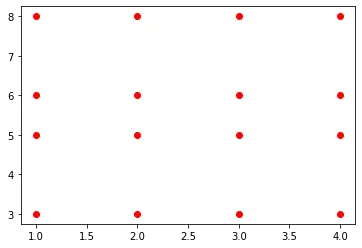
Bien sûr, meshgrid est généralement utilisé pour des tâches plus complexes qui prendraient une éternité si elles étaient effectuées avec des boucles. Le tracé d’un graphique de contour de la fonction sinusoïdale 3D en est un exemple :
def sinus2d(x, y):
return np.sin(x) + np.sin(y)
xx, yy = np.meshgrid(np.linspace(0, 2 * np.pi, 100), np.linspace(0, 2 * np.pi, 100))
z = sinus2d(xx, yy) # Créer l'image sur cette grille
import matplotlib.pyplot as plt
plt.imshow(z, origin="lower", interpolation="none")
plt.show()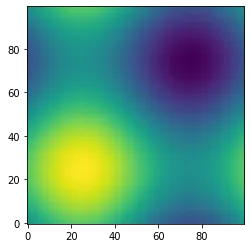
Documentation de meshgrid.
4. np.triu / np.tril
Tout comme ones_like ou zeros_like, ces deux fonctions renvoient des zéros au-dessus ou au-dessous d’une certaine diagonale d’une matrice. Par exemple, nous pouvons utiliser la fonction triu pour créer un masque booléen avec des valeurs True au-dessus de la diagonale principale et utiliser ce masque pour tracer une carte thermique de corrélation.
import seaborn as sns
diamonds = sns.load_dataset("diamonds")
matrix = diamonds.corr()
mask = np.triu(np.ones_like(matrix, dtype=bool))
sns.heatmap(matrix, square=True, mask=mask, annot=True, fmt=".2f", center=0);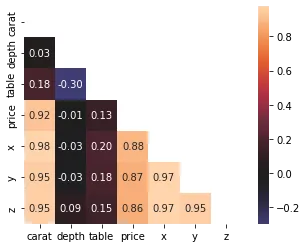
Comme tu peux le voir, un masque créé avec triu peut être utilisé sur une matrice de corrélation pour supprimer le triangle supérieur et la diagonale inutiles. Il en résulte une carte thermique beaucoup plus compacte et lisible, dépourvue d’encombrement.
Documentation de triu.
5. np.ravel / np.flatten
NumPy, c’est tout ce qui concerne les matrices et les ndarrays à haute dimension. Parfois, tu veux simplement prendre ces tableaux et les écraser en 1D. C’est là que tu utilises ravel ou flattant :
array = np.random.randint(0, 10, size=(4, 5))
>>> array
array([[6, 4, 8, 9, 6],
[5, 0, 4, 8, 5],
[1, 3, 1, 0, 3],
[2, 3, 3, 6, 5]])
>>> array.ravel()
array([6, 4, 8, 9, 6, 5, 0, 4, 8, 5, 1, 3, 1, 0, 3, 2, 3, 3, 6, 5])
>>> array.flatten()
array([6, 4, 8, 9, 6, 5, 0, 4, 8, 5, 1, 3, 1, 0, 3, 2, 3, 3, 6, 5])Se ressemblent-ils ? Pas exactement. flatten renvoie toujours une copie 1D alors que ravel essaie de produire une vue 1D du tableau d’origine. Il faut donc faire attention car modifier le tableau retourné par ravel peut modifier le tableau d’origine.
Pour plus d’informations sur leurs différences, consulte ce thread StackOverflow. Et également la documentation de ravel.
6. np.vstack / np.hstack
Sur Kaggle, ces deux fonctions sont régulièrement utilisées. Souvent, les gens ont plusieurs prédictions pour l’ensemble de test provenant de différents modèles, et ils veulent regrouper ces prédictions d’une manière ou d’une autre. Pour faciliter leur utilisation, elles doivent être combinées en une seule matrice.
array1 = np.arange(1, 11).reshape(-1, 1)
array2 = np.random.randint(1, 10, size=10).reshape(-1, 1)
hstacked = np.hstack((array1, array2))
>>> hstacked
array([[ 1, 2],
[ 2, 6],
[ 3, 6],
[ 4, 7],
[ 5, 4],
[ 6, 6],
[ 7, 6],
[ 8, 8],
[ 9, 2],
[10, 8]])
array1 = np.arange(20, 31).reshape(1, -1)
array2 = np.random.randint(20, 31, size=11).reshape(1, -1)
vstacked = np.vstack((array1, array2))
>>> vstacked
array([[20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30],
[21, 23, 23, 26, 29, 26, 27, 27, 28, 25, 25]])N’oublie pas de remodeler (reshape) chaque tableau avant de les empiler avec ceux-ci, car ils requièrent par défaut des tableaux en 2D. C’est pourquoi nous avons utilisé la fonction reshape. Ici, reshape(-1, 1) représente la conversion du tableau en une seule colonne avec autant de lignes que possible.
De même, reshape(1, -1) convertit le tableau en un vecteur d’une seule ligne avec autant de colonnes que possible.
Documentation de hstack.
7. np.r_ / np.c_
Si tu es paresseux comme moi et que tu ne veux pas appeler reshape sur tous tes tableaux, il existe une solution beaucoup plus élégante. Les opérateurs np.r_ et np.c_ (pas des fonctions !) permettent d’empiler des tableaux en lignes et en colonnes, respectivement.
Ci-dessous, nous simulons un tableau de prédiction avec 100 probabilités. Pour les empiler les unes sur les autres, nous appelons np.r_ avec la notation entre crochets (comme pandas.DataFrame.loc).
preds1 = np.random.rand(100) preds2 = np.random.rand(100) as_rows = np.r_[preds1, preds2] as_cols = np.c_[preds1, preds2] >>> as_rows.shape (200,) >>> as_cols.shape (100, 2)
De même, np.c_ empile les tableaux les uns à côté des autres, créant ainsi une matrice. Cependant, leur fonctionnalité ne se limite pas à de simples empilements horizontaux et verticaux. Elles sont bien plus puissantes que cela. Pour plus d’informations, je te suggère de lire les documentations :
8. np.info
NumPy est tellement vaste et profond. Tu n’auras probablement pas le temps et la patience d’apprendre chaque fonction et chaque classe de son API. Que faire si tu es confronté à une fonction inconnue ? Eh bien, ne te précipite pas sur la documentation car tu as une bonne alternative.
La fonction information permet d’imprimer la docstring de n’importe quel nom de l’API NumPy. Voici info utilisé sur info :
>>> np.info(np.info)
info(object=None, maxwidth=76,
output=<ipykernel.iostream.OutStream object at 0x0000021B875A8820>,
toplevel='numpy')
Get help information for a function, class, or module.
Parameters
----------
object : object or str, optional
Input object or name to get information about. If `object` is a
numpy object, its docstring is given. If it is a string, available
modules are searched for matching objects. If None, information
about `info` itself is returned.
maxwidth : int, optional
Printing width.
....Documentation de info.
9. np.where
Comme son nom l’indique, cette fonction renvoie tous les indices d’un tableau où (where) une certaine condition est True :
probs = np.random.rand(100)
idx = np.where(probs > 0.8)
>>> probs[idx]
array([0.80444302, 0.80623093, 0.98833642, 0.96856382, 0.89329919,
0.88664223, 0.90515148, 0.96363973, 0.81847588, 0.88250337,
0.98737432, 0.92104315])Elle est particulièrement utile lors de la recherche d’éléments non nuls dans des tableaux peu denses ou peut même être utilisée sur des DataFrames Pandas pour une recherche d’index beaucoup plus rapide basée sur une condition. Documentation de where.
10. np.all / np.any
Ces deux fonctions seront très utiles lors du nettoyage des données lorsqu’elles sont utilisées avec des instructions assert.
np.all renvoie uniquement True si tous les éléments d’un tableau correspondent à une condition spécifique :
array1 = np.random.rand(100) array2 = np.random.rand(100) >>> np.all(array1 == array2) False
Comme nous avons créé deux tableaux remplis de nombres aléatoires, il n’y a aucune chance que tous les éléments soient égaux. Cependant, il y a beaucoup plus de chances qu’au moins deux d’entre eux soient égaux si les nombres sont des entiers :
a1 = np.random.randint(1, 100, size=100) a2 = np.random.randint(1, 100, size=100) >>> np.any(a1 == a2) True
Ainsi, any renvoie True si au moins un élément d’un tableau satisfait à une condition particulière. Pour plus d’informations, je te suggère de lire les documentations :
11. np.allclose
Si tu souhaites vérifier si deux tableaux de même longueur sont des copies l’un de l’autre, un simple opérateur == ne suffira pas. Il peut arriver que tu souhaites comparer des tableaux de nombres flottants, mais leurs longues décimales rendent la tâche difficile. Dans ce cas, tu peux utiliser allclose qui renvoie True si tous les éléments d’un tableau sont proches les uns des autres, compte tenu d’une certaine tolérance.
a1 = np.arange(1, 10, step=0.5)
a2 = np.arange(0.8, 9.8, step=0.5)
>>> np.all(a1 == a2)
False
>>> a1
array([1. , 1.5, 2. , 2.5, 3. , 3.5, 4. , 4.5, 5. , 5.5, 6. , 6.5, 7. ,
7.5, 8. , 8.5, 9. , 9.5])
>>> a2
array([0.8, 1.3, 1.8, 2.3, 2.8, 3.3, 3.8, 4.3, 4.8, 5.3, 5.8, 6.3, 6.8,
7.3, 7.8, 8.3, 8.8, 9.3])
>>> np.allclose(a1, a2, rtol=0.2)
False
>>> np.allclose(a1, a2, rtol=0.3)
TrueNote que la fonction renvoie True uniquement si les différences sont inférieures (<) à rtol, et non <= ! Tu peux consulter la documentation de allclose pour plus d’information.
12. np.argsort
Bien que np.sort renvoie une copie triée d’un tableau, ce n’est pas toujours ce que tu veux. Parfois, tu as besoin des indices qui trieraient un tableau pour utiliser les mêmes indices plusieurs fois à des fins différentes. C’est là que argsort s’avère utile :
random_ints = np.random.randint(1, 100, size=20)
idx = np.argsort(random_ints)
>>> random_ints[idx]
array([ 6, 19, 22, 23, 35, 36, 37, 45, 46, 57, 61, 62, 64, 66, 66, 68, 72,
74, 87, 89])Elle fait partie d’une famille de fonctions commençant par arg, qui renvoient toujours un ou plusieurs indices du résultat d’une fonction. Par exemple, argmax trouve la valeur maximale d’un tableau et renvoie son indice.
Documentation de argsort.
13. np.isneginf / np.isposinf
Ces deux fonctions booléennes vérifient si un élément d’un tableau est moins l’infini ou plus l’infini. Malheureusement, les ordinateurs ou NumPy ne comprennent pas le concept d’infini (enfin, qui le comprend ?). Ils ne peuvent représenter l’infini que sous la forme d’un nombre extrêmement grand ou petit qu’ils peuvent faire tenir dans un seul bit (j’espère que je l’ai dit correctement).
C’est pourquoi lorsque tu imprimes le type de np.inf, il renvoie float :
>>> type(np.inf) # type de l'infini float >>> type(-np.inf) float
Cela signifie que les valeurs infinies peuvent facilement se faufiler dans un tableau et casser les opérations que tu utiliserais sur les flottants. Tu as besoin d’une fonction spéciale pour trouver ces petites valeurs sournoises… :
a = np.array([-9999, 99999, 97897, -79897, -np.inf]) >>> np.all(a.dtype == "float64") True >>> np.any(np.isneginf(a)) True
Documentation de isneginf.
14. np.polyfit
Si tu souhaites effectuer une régression linéaire traditionnelle, tu n’as pas nécessairement besoin de Sklearn. NumPy te couvre :
X = diamonds["carat"].values.flatten() y = diamonds["price"].values.flatten() slope, intercept = np.polyfit(X, y, deg=1) >>> slope, intercept (7756.425617968436, -2256.3605800454034)
polyfit peut prendre deux vecteurs, leur appliquer une régression linéaire et renvoyer une pente et une ordonnée à l’origine. Il suffit de spécifier le degré avec deg, car cette fonction peut être utilisée pour approximer les racines de n’importe quel polynôme de degré.
Une double vérification avec Sklearn révèle que la pente et l’ordonnée à l’origine trouvées avec polyfit sont les mêmes que le modèle LinearRegression de Sklearn :
from sklearn.linear_model import LinearRegression lr = LinearRegression().fit(X.reshape(-1, 1), y) >>> lr.coef_, lr.intercept_ (array([7756.42561797]), -2256.360580045441)
Documentation de polyfit.
15. Distributions de probabilités
Le module random de NumPy dispose d’une large sélection de générateurs de nombres pseudo-aléatoires. En plus de mes favoris tels que sample et choice, il existe des fonctions pour simuler des distributions de probabilités pseudo-parfaites.
Par exemple, les fonctions binomial, gamma, normal et tweedie tirent un nombre personnalisé de points de données de leurs distributions respectives.
Ces fonctions peuvent s’avérer très utiles lorsque tu dois approximer les distributions des features de tes données. Par exemple, nous vérifions ci-dessous si les prix des diamants suivent une distribution normale.
fig, ax = plt.subplots(figsize=(6, 8)) price_mean = diamonds["price"].mean() price_std = diamonds["price"].std() # Tracé d'une distribution normale parfaite perfect_norm = np.random.normal(price_mean, price_std, size=1000000) sns.kdeplot(diamonds["price"], ax=ax) sns.kdeplot(perfect_norm, ax=ax) plt.legend(["Price", "Perfect Normal Distribution"]);
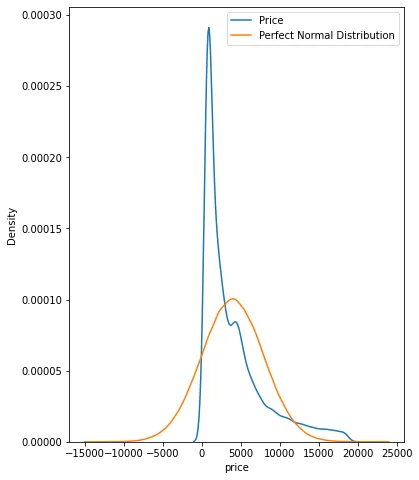
Pour ce faire, on peut tracer un KDE des prix des diamants au-dessus d’une distribution normale parfaite afin de faire apparaître les différences.
Documentation de random.
16. np.rint
rint est une petite fonction très pratique qui permet d’arrondir chaque élément d’un tableau à l’entier le plus proche. Tu peux commencer à l’utiliser lorsque tu souhaites convertir les probabilités de classe en étiquettes de classe dans la classification binaire. Tu n’as pas besoin d’appeler la méthode predict de ton modèle, ce qui te fait perdre du temps :
preds = np.random.rand(100)
>>> np.rint(preds[:50])
array([1., 1., 0., 1., 0., 1., 1., 0., 0., 0., 0., 1., 0., 1., 0., 1., 0.,
1., 0., 1., 1., 1., 1., 1., 0., 0., 1., 0., 0., 0., 0., 1., 0., 0.,
0., 0., 0., 0., 0., 0., 1., 0., 1., 0., 1., 1., 0., 0., 1., 0.])Documentation de rint.
17. np.nanmean / np.nan*
Sais-tu que les opérations arithmétiques sur les tableaux NumPy purs échouent si au moins un élément est NaN ?
a = np.array([12, 45, np.nan, 9, np.nan, 22]) >>> np.mean(a) nan
Pour contourner ce problème sans modifier le tableau d’origine, tu peux utiliser une famille de fonctions nan :
>>> np.nanmean(a) 22.0
Voici un exemple de la fonction de moyenne arithmétique qui ignore les valeurs manquantes. De nombreuses autres fonctions fonctionnent de la même manière :
>>> [func for func in dir(np) if func.startswith("nan")]
['nan',
'nan_to_num',
'nanargmax',
'nanargmin',
'nancumprod',
'nancumsum',
'nanmax',
'nanmean',
'nanmedian',
'nanmin',
'nanpercentile',
'nanprod',
'nanquantile',
'nanstd',
'nansum',
'nanvar']Mais tu peux tout aussi bien les oublier si tu ne travailles qu’avec des DataFrames ou des Series Pandas, car ils ignorent les NaNs par défaut.
>>> pd.Series(a).mean() 22.0
Documentation de nanmean.
18. np.clip
clip est utile lorsque tu souhaites imposer une limite stricte aux valeurs de votre tableau. Ci-dessous, nous écrêtons toutes les valeurs qui se trouvent en dehors des limites strictes de 10 et 70 :
ages = np.random.randint(1, 110, size=100)
limited_ages = np.clip(ages, 10, 70)
>>> limited_ages
array([13, 70, 10, 70, 70, 10, 63, 70, 70, 69, 45, 70, 70, 56, 60, 70, 70,
10, 52, 70, 32, 62, 21, 70, 13, 13, 10, 50, 38, 32, 70, 20, 27, 64,
34, 10, 70, 70, 53, 70, 53, 54, 26, 70, 57, 70, 46, 70, 17, 48, 70,
15, 49, 70, 10, 70, 19, 23, 70, 70, 70, 45, 47, 70, 70, 34, 25, 70,
10, 70, 42, 62, 70, 10, 70, 23, 25, 49, 70, 70, 62, 70, 70, 11, 10,
70, 30, 44, 70, 49, 10, 35, 52, 21, 70, 70, 25, 10, 55, 59])Documentation de clip.
19. np.count_nonzero
Il est courant de travailler avec des tableaux peu denses. Souvent, ils résultent de l’encodage d’une feature catégorielle avec une cardinalité élevée ou de nombreuses colonnes binaires.
Tu peux vérifier le nombre d’éléments non nuls dans un tableau avec count_nonzero :
a = np.random.randint(-50, 50, size=100000) >>> np.count_nonzero(a) 98993
Parmi 100k entiers aléatoires, ~1000 d’entre eux sont des zéros.
Documentation de count_nonzero.
20. np.array_split
La dernière fonction de notre liste est array_split. Je pense que tu peux deviner ce qu’elle fait d’après son nom – elle peut être utilisée pour diviser des ndarrays ou des DataFrames en N buckets. De plus, elle ne soulève pas d’erreur lorsque tu veux diviser le tableau en morceaux de taille inégale comme vsplit :
import datatable as dt
df = dt.fread("data/train.csv").to_pandas()
splitted_dfs = np.array_split(df, 100)
>>> len(splitted_dfs)
100Documentation de array_split.
Même si l’on ne passe généralement pas beaucoup de temps à travailler directement avec NumPy, le fait d’avoir quelques astuces dans sa manche peut rendre tes sessions de code NumPy beaucoup plus agréables et fluides. N’oublie pas une chose : certaines astuces NumPy sont assez avancées, tu dois donc trouver un équilibre entre la lisibilité, la flexibilité et les contraintes de temps.